フェルマーの原理
フェルマーの原理(最小時間の原理)とは、以下のように言い表すことができます。
- 実際の光の経路は、光の伝播に要する時間が最小となる経路である。
- 実際の光の経路は、光学的距離が最小となるような経路である。
区間 $AB$ 間の光学的距離を $L_{AB}$ 、光の伝播に要する時間を $T_{AB}$ 、真空中の高速度を $c$ とすると、以下で表すことができます。
$$L_{AB}=cT_{AB} -①$$
尚、光学的距離とは、任意の屈折率を持つ媒質中を光が走るのに要する時間と同じ時間内に真空中を光が走ることのできる距離です。
①の導出
媒質1の区間 $ds$ の光の速度 $c(s)$ を、その区間を光が通過する時間 $dt$ をとすると、
$$dt=\frac{ds}{c(s)}$$
区間 $AB$ を光が通過する時間 $T_{AB}$ は、
$$T_{AB}=\int_A^Bdt=\int_A^B\frac{ds}{c(s)}$$
スネルの法則より、区間 $ds$ の屈折率を $n(s)$ とすると、
$$n(s)c(s)=c$$
これを代入し、②を利用すると①が得られます。
$$T_{AB}=\int_A^B\frac{n(s)}{c}ds=\frac{L_{AB}}{c}$$
光学的距離
光学的距離 $L$ は、光の経路の微小区間を $ds$ 、その屈折率を $n$ とすると、以下で求められます。
$$L_{AB}=\int n(s)ds -②$$
光学的距離は、媒質(屈折率)や実際の距離に関係なく一定であることが分かります。
②の導出
媒質1から媒質2への入射光の経路 $ABCD$ と $A’B’C’D’$ を考えます。ここで $AA’$ 、$BB’$ 、$CC’$ 、$DD’$ は等位相波面を表します。
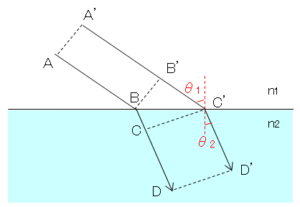
図より、経路 $BC$ 、$B’C’$ と入射角 $\theta$ との関係は以下で表されます。
$$\frac{\overline{B’C’}}{\sin{\theta_1}}=\frac{\overline{BC}}{\sin{\theta_2}}=\overline{BC’}$$
このとき $\overline{BC}$ と $\overline{B’C’}$ はそれぞれの媒質の波長 $\lambda$ に比例すると考えられるため、以下のように書き換えられ、
$$\frac{\lambda_1}{\sin{\theta_1}}=\frac{\lambda_2}{\sin{\theta_2}} -③$$
一方、スネルの法則より、
$$n_1\sin{\theta_1}=n_2\sin{\theta_2}$$
が成り立つため、③は以下のように表されます。$\lambda$ は真空中(屈折率は $1$ )の波長です。
$$n_1\lambda_1=n_2\lambda_2=\lambda -④$$
距離を波長で割ったものは波数ですが、経路 $ABCD$ と $A’B’C’D’$ の波数は等しいため、
$$\frac{\overline{AB}}{\lambda_1}+\frac{\overline{BD}}{\lambda_2}=\frac{\overline{A’C’}}{\lambda_1}+\frac{\overline{C’D’}}{\lambda_2}$$
これに④を代入すると、
$$\frac{n_1\overline{AB}}{\lambda}+\frac{n_2\overline{BD}}{\lambda}=\frac{n_1\overline{C’B’}}{\lambda}+\frac{n_2\overline{C’D’}}{\lambda}$$
従って、光学的距離 $L$ を以下で定義すると、
$$L=n_1\overline{AB}+n_2\overline{BD}=n_1\overline{C’B’}+n_2\overline{C’D’}$$
区間を小さく分割して足し合わせると、$L$ が媒質(屈折率)や実際の距離に関係なく一定であることが分かります。
$$L=\lim_{\Delta s\to0}\sum_in_i\Delta s_i$$



