資本資産価格モデルとは
資本資産価格モデル(Capital Asset Pricing Model、以下、CAPM)とは、ある仮定の下、リスク資産の期待投資収益率と価格がどのように決定されるか示したものです。CAPMでは、以下の仮定を設けています。
- 全ての投資家は合理的(リスク回避者)である
- 全ての投資家はリターンとリスクのみで判断する
- 市場には無リスク資産が存在し、十分な貸借ができる
- 市場は完全市場である
(=取引手数料や税金はなく、株式は無限に分割でき、投資家の取引は市場価格に影響を与えない等)
上記のような過程を置くと、全ての投資家のリスク資産ポートフォリオは「市場ポートフォリオ」と同一になるという結論に至ります。市場ポートフォリオとは、各リスク資産の割合が時価総額の比率と同一のポートフォリオです。
全ての投資家は合理的な判断を行うため、その個別銘柄の投資比率は同一となり、市場全体もそれと同じ比率となります。そのため、全ての投資家の投資比率は、全ての市場に存在する時価総額の比率と同一になります。
完全で効率的な市場においては、投資家は市場ポートフォリオを上回るリターンを得ることはできません。そのため、この理論はインデックス投資の理論的裏付けとなっています。つまり、全ての投資家とって、「接点ポートフォリオ=市場ポートフォリオ」となります。
資本市場線
資本市場線(Capital Market Line、以下、CML)とは、無リスク資産と市場ポートフォリオを結んだ直線です。最適ポートフォリオはCML上にあるため、投資家は無リスク資産とリスク資産で構成されるポートフォリオ(市場ポートフォリオ)との投資割合のみ検討すればよいことになります。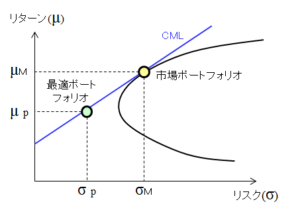
リスクの市場価格とはCMLの傾きで、市場ポートフォリオの期待収益率 $\mu_M$ と標準偏差 $\sigma_M$ 、無リスク資産の金利 $R_f$ により以下で求められます。
$$\mbox{リスクの市場価格}=\frac{\mu_M-R_f}{\sigma_M}$$
従って、最適ポートフォリオの期待収益率 $\mu_p$ は以下で表されます。ここで $\sigma_p$ は最適ポートフォリオの標準偏差です。
$$\mu_p=R_f+\frac{\mu_M-R_f}{\sigma_M}\sigma_p$$
この式は、リスクを負担することにより、無リスク金利を上回る超過リターンを得ることができることを示しています。
証券市場線
証券市場線(Security Market Line、以下、SML)とは、横軸を $\beta$(システマチックリスク)、縦軸を期待収益率としたグラフで、無リスク資産と市場ポートフォリオを結んだ直線です。個別リスク資産と市場が均衡状態にある場合、個別リスク資産の期待投資収益率はSML上に位置します。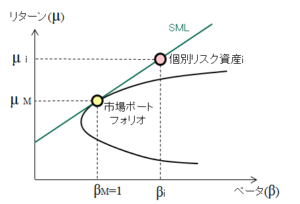
個別リスク資産 $i$ の投資収益率 $\mu_i$ は以下で求められます。
$$\mu_i=R_f+\beta_i(\mu_M-R_f)$$
$\beta_i$ は市場ポートフォリオのリスクに対する個別リスク資産のリスクの比であるため、$\mu_i$ は個別リスク資産のリスクに見合った投資収益率の理論値と考えることができます。
ポートフォリオの評価指標
以下のパフォーマンス評価指標は、資本市場線(CML)と証券市場線(SML)が均衡価格を表すことを前提にしており、投資対象のポートフォリオをリスクに見合ったリターンが得られているかという観点で評価しています。
シャープレシオ
シャープレシオとは、リスクに対するリターンの大きさを示す指標です。ポートフォリオの投資収益率 $\mu_A$ と標準偏差 $\sigma_A$ 、無リスク金利 $R_f$ より、以下で求められます。
$$\mbox{シャープレシオ}=\frac{\mu_A-R_f}{\sigma_A}$$
シャープレシオが大きいほど、投資効率が良い(同じリスクでリターンが大きい)と言えます。また、CMLと比較して、左上であれば市場より投資効率が良く、右下であればその逆であることが言えます。
トレイナー尺度
トレイナー尺度とは、リスクに対するリターンの大きさを示す指標です。シャープレシオと異なり、リスクの尺度として $\beta$(システマチックリスク)を用います。
$$\mbox{トレイナー尺度}=\frac{\mu_A-R_f}{\beta_A}$$
トレイナー尺度が大きいほど、投資効率が良い(同じリスクでリターンが大きい)と言えます。また、SMLと比較して、左上であれば市場より投資効率が良く、右下であればその逆であることが言えます。
ジェンセンの $\alpha$
ジェンセンの $\alpha$(アルファ)は、個別リスク資産のポートフォリオと証券市場線(SML)との収益率の差を測る指標で、個別リスク資産の投資収益率(実績値)が証券市場線(理論値)をどの程度上回った(下回ったか)を示します。
$$\alpha=\mu_A-\Big(R_f+\beta_A(\mu_M-R_f)\Big)$$
ジェンセンの $\alpha$(アルファ)が正であれば、市場ポートフォリオより優れたパフォーマンスであり、負であれば、市場ポートフォリオより劣ったパフォーマンスであると評価できます。




