図形と方程式（高校数学）

図形と計算（数学Ⅰ）

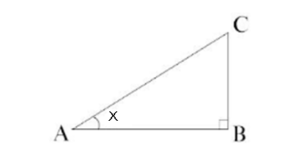
三角比の定義

三角比（三角関数）は以下で定義されます。

$$\sin{x}=\frac{BC}{AC}$$$$\cos{x}=\frac{AB}{AC}$$$$\tan{x}=\frac{BC}{AB}$$

正弦定理

三角形 $ABC$ の各角に対する辺を $a,b,c$ とし、外接円の半径を $R$ とすると、以下の関係が成り立ちます。

$$\frac{a}{\sin{A}}=\frac{b}{\sin{B}}=\frac{c}{\sin{C}}=2R$$

［左辺の導出］
点 $C$ から辺 $AB$ に下した垂線との交点を $C’$ とすると、$|CC’|=b\sin{A}=a\sin{B}$ より得られます。

［右辺の導出］
下左図は $C\lt\pi/2$ の場合です。$A$ から円の中心を通る線分を $AD$ とすると、$\angle ABD$ は直角であるため $c=2R\sin{\angle ADB}$ となります。円周角より $C=\angle ADB$ であるため、$c=2R\sin{\angle ADB}=2R\sin{C}$ が得られます。

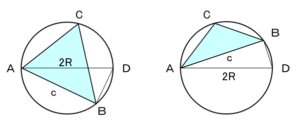
上右図は $C\gt\pi/2$ の場合です。$A$ から円の中心を通る線分を $AD$ とすると、$\angle ABD$ は直角であるため $c=2R\sin{\angle ADB}$ となります。円に内接する四角形の対角は $C+\angle ADB=\pi$ であるため、$c=2R\sin{\angle ADB}=2R\sin{(\pi-C)}=2R\sin{C}$ が得られます。

余弦定理

三角形 $ABC$ の各角に対する辺を $a,b,c$ とすると、以下の関係が成り立ちます。

$a^2=b^2+c^2-2bc\cos{A}$
$b^2=c^2+a^2-2ca\cos{B}$
$c^2=a^2+b^2-2ab\cos{C}$
$a=c\cos{B}+b\cos{C}$
$b=a\cos{C}+c\cos{A}$
$c=b\cos{A}+a\cos{B}$

［1. の導出］
各辺のベクトルを ${\bf a},{\bf b},{\bf c}$ で表わすと、${\bf a}={\bf b}-{\bf b}$ より、両辺を２乗すると得られます。
$|{\bf a}|^2=({\bf b}-{\bf c})^2=|{\bf b}|^2+|{\bf c}|^2-2{\bf b}\cdot{\bf c}=b^2+c^2-2bc\cos{A}$

［2. の導出］
点 $A$ から辺 $BC$ に下した垂線との交点を $A’$ とすると、$|BA’|=c\cos{B}$ 、$|CA’|=b\cos{C}$ となり、$|BA’|+|CA’|=a$ であることから得られます。

三角形の角と辺の関係

三角形 $ABC$ の各角に対する辺を $a,b,c$ とすると、

三角形の成立条件：$|b-c|\lt a\lt b+c$

以下の大小関係が成り立ちます。

$A\lt$ 90° ならば、$a^2\lt b^2+c^2$
$A=$ 90° ならば、$a^2=b^2+c^2$
$A\gt$ 90° ならば、$a^2\gt b^2+c^2$

三角形の面積

三角形 $ABC$ の各角に対する辺を $a,b,c$ とすると、面積は以下で表されます。

$$S=\frac{1}{2}bc\sin{A}=\frac{1}{2}ca\sin{B}=\frac{1}{2}ab\sin{C}$$

ヘロンの公式は、$2s=a+b+c$ と置くと以下で表されます。

$$S=\sqrt{s(s-a)(s-b)(s-c)}$$

三角形の面積は、内接円の半径を $r$ とすると以下で表されます。

$$S=\frac{1}{2}r(a+b+c)$$

図形の性質（数学Ａ）

二等分線の比

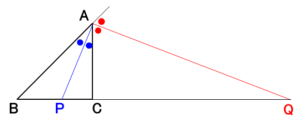
三角形 $ABC$ について、

角 $A$ の二等分線が辺 $BC$ と交わる点を $P$ とすると、
$BP:PC=AB:AC$ が成り立つ。
角 $A$ の外角の二等分線が辺 $BC$ の延長と交わる点を $Q$ とすると、
$BQ:QC=AB:AC$ が成り立つ。

重心・外心・垂心・内心

各定義は以下になります。

重心：三角形の３つの角と対辺の二等分点を結ぶ直線（中線）が交わる点。
外心：三角形の３辺の垂直二等分線が交わる点。
内心：三角形の３つの内角の二等分線が交わる点。
垂心：三角形の３つの角から対辺に下した垂線が交わる点。

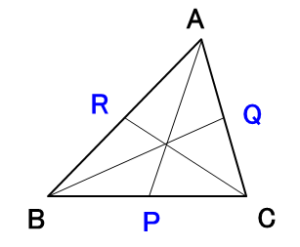
チェバの定理

三角形 $ABC$ の３辺 $BC,CA,AB$ 上にそれぞれ点 $P,Q,R$ があり、３つの直線が１点で交わるとき、以下の関係が成り立ちます。

$$\frac{BP}{PC}\cdot\frac{CQ}{QA}\cdot\frac{AR}{RB}=1$$

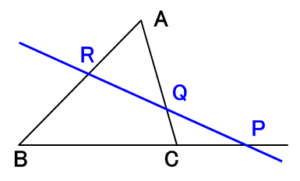
メネラウスの定理

メネラウスの定理は、ある直線が三角形 $ABC$ の３辺 $BC,CA,AB$ またはその延長とそれぞれ点 $P,Q,R$ で交わるとき、以下の関係が成り立つことを示します。

$$\frac{BP}{PC}\cdot\frac{CQ}{QA}\cdot\frac{AR}{RB}=1$$

円に内接する四角形

円に内接する四角形では以下が成り立ちます。

対角の和は180° である。
内角は、その対角の外角に等しい。

円周角と接弦定理

円に内接する三角形について以下の関係が成り立ちます。

弦 $AB$ に対する円周角（$\angle ACB$ 、$\angle ADB$ ）は等しい。
弦 $AB$ が直径の場合、円周角は直角になる。
接弦定理：円の接点 $A$ とその接点を通る弦 $AB$ による角 $\angle BAE$ と円周角は等しい。

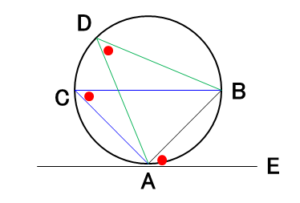
方べきの定理

点 $P$ を通る２直線について、以下の定理が成り立ちます。この定理は、その逆も成り立ちます。

円とそれぞれ２点 $A,B$ と２点 $C,D$ で交わるとき、
$PA\cdot PB=PC\cdot PD$
一方の直線が円と２点 $A,B$ で交わり、もう一方の直線が点 $T$ で接するとき、
$PA\cdot PB=PT^2$

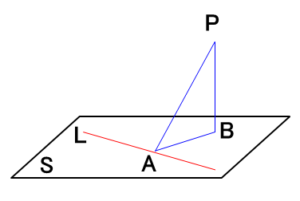
三垂線の定理

平面 $S$ 上に直線 $L$ があるとき、$L$ 上の点 $A$ 、$L$ 上にない $S$ 上の点 $B$ 、$S$ 上にない点 $P$ について、

$PB\perp S$ 、$AB\perp L$ ならば、$PA\perp L$
$PB\perp S$ 、$PA\perp L$ ならば、$AB\perp L$
$PA\perp L$ 、$AB\perp L$ 、$PB\perp AB$ ならば、$PB\perp S$

オイラーの多面体定理

凸多面体の頂点の数を $a$ 、辺の数を $b$ 、面の数を $c$ とすると以下の関係が成り立ちます。

$$a-b+c=2$$

図形と方程式（数学Ⅱ）

点の座標

３点 $A(x_1,y_1),B(x_2,y_2),C(x_3,y_3)$ において、

内分点：線分 $AB$ を $m:n$ に内分する点
$$\Big(\frac{nx_1+mx_2}{m+n},\frac{ny_1+my_2}{m+n}\Big)$$
外分点：線分 $AB$ を $m:n$ に外分する点
$$\Big(\frac{-nx_1+mx_2}{m-n},\frac{-ny_1+my_2}{m-n}\Big)$$
重心：三角形の重心は、
$$\Big(\frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3}\Big)$$

直線の方程式

直線の方程式は以下で表されます。

直線の方程式の一般形
$$ax+by+c=0$$
点（$x_1,y_1$）を通り、傾き $a$ の直線の方程式
$$y-y_1=a(x-x_1)$$
２点（$x_1,y_1$）､（$x_2,y_2$）を通る方程式
$$y-y_1=\frac{y_2-y_1}{x_2-x_1}(x-x_1)$$

２直線 $y=ax+b$、$y=a’x+b’$ について、

交わる条件：$a\ne a’$
平行条件：$a=a’$
垂直条件：$aa’=-1$

距離と面積

２点間の距離：
２点 $(x_1,y_1)$ ､ $(x_2,y_2)$ 間の距離 $d$ は、
$$d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$$
点と直線の距離：
点 $(x_1,y_1)$ と直線 $ax+by+c=0$ の距離 $d$ は、
$$d=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}$$
三角形の面積：
原点と２点 $(x_1,y_1)$ ､ $(x_2,y_2)$ を頂点とする三角形の面積 $S$ は、
$$S=\frac{1}{2}|x_1y_2-x_2y_1|$$