電界効果トランジスタ
電界効果トランジスタ(Field effect transistor、以下、FET)とは、半導体の内部に生じる電界によって電流を制御する方式のトランジスタです。
バイポーラのトランジスタがキャリアとして電子と正孔の両方を制御するのに対し、FET(ユニポーラ)は電子または正孔の一方を制御します。このキャリアが電子であればN型チャネルFET、正孔であればP型チャネルFETに分類されます。
FETの3つの端子はそれぞれ、ソース(Source)、ドレイン(Drain)、ゲート(Gate)と呼ばれます。ゲートがPN接合であれば接合型、MOS構造(金属・酸化物・半導体の層状構造)であればMOS型に分類されます。
ゲート電圧を掛けたときにドレイン電流が流れるものをエンハンスメント(ノーマリOFF)、ゲート電圧を掛けないときもドレイン電流が流れるものをデュプレッション(ノーマリON)に分かれます。MOS型のほとんどがエンハンスメント、接合型のほとんどがデュプレッションです。
接合型FET
接合型FETのP型チャネルとN型チャネルの回路記号は以下になります。
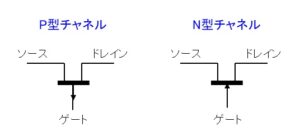
構造と仕組み
N型チャネルの接合型FETの構造を以下に示します。P型チャネルの場合は、PNおよび電圧の極性入れ替えたものなります。
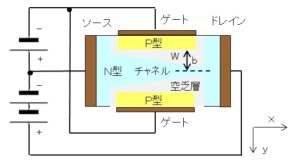
この場合、ソースに負電圧、ドレインに正電圧が掛かるため、キャリヤ(電子)はソースからドレインに流れます(ドレイン電流)。
ゲートには負電圧がかかっており、ゲートとチャネル間のPN接合は逆電圧になるため空乏層ができます。ドレインには正の電圧がかかっているため、ドレイン側の空乏層の幅が大きくなります。
空乏層はゲート電圧 $V_G$ とドレイン電圧 $V_D$ により幅が変わるため、ドレイン電流 $I_D$ を制御することができます。このときゲート電流はほとんど流れないため、バイポーラのトランジスタより、真空管に似た特性を持ちます。
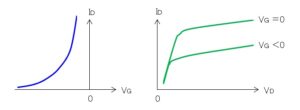
- ゲートの負電圧を上げると空乏層の幅が大きくなり、ドレイン電流は減少する。ゲートの負電圧を下げると空乏層の幅は小さくなり、ドレイン電流は増加する。
- ゲートの負電圧をさらに大きくすると空乏層がさらに広がり、チャネルは閉じられ(ピンチオフ)、この状態ではドレイン電流は飽和状態になる。
- ドレイン電圧を大きくするとドレイン電流が増加するが、ドレイン側の空乏層が広がるため、ドレイン電流は飽和し一定となる(ピンチオフ)。
電流特性
接合型FETの電流特性を導きます。ソースからドレインの方向に $x$ 軸、図の下方向に $y$ 軸をとり、空乏層の幅を $W$ 、チャネルの長さを $a$ 、P型半導体間の幅を $2b$ 、$z$ 軸方向の幅を $c$ とします。
PN接合のモデルより、N型半導体(N型FET)の空乏層は以下で与えられます。ここで、$N_d$ はドナーの密度、$e$ は電気素量、$\epsilon$ は誘電率を表します。
$$W(x)=\sqrt{\frac{2\epsilon\Delta\phi}{eN_d}}$$
$\Delta\phi$ はPN接合の内蔵電位差ですが、外部から電圧を掛けることで空乏層は大きくなります。$V_G(\lt 0)$ はゲート電圧、$V(x)$ はチャネルの電圧を表します。
$$W(x)=\sqrt{\frac{2\epsilon}{eN_d}\big(\Delta\phi-V_G+V(x)\big)} -①$$
ドレイン電流 $I_D$ とゲート電圧 $V_G$ およびドレイン電圧 $V_D$ の関係は以下で与えられます。(②の導出)
$$I_D=\frac{2z_0}{a\eta}\left(bV_D-\frac{2}{3}\sqrt{\frac{2\epsilon}{eN_d}}\Big((\Delta\phi-V_G+V_D)^{3/2}-(\Delta\phi-V_G)^{3/2}\Big)\right) -②$$
ピンチオフが起きたときの空乏層の幅は $W(x)=b$ となるため、ドレイン電圧を $V(x)=V_p$(ピンチオフ電圧)とすると①より、
$$b=\sqrt{\frac{2\epsilon}{eN_d}\big(\Delta\phi-V_G+V_p\big)} -③$$
これによりピンチオフ時の飽和ドレイン電流は以下で得られます。ここで $\eta$ は抵抗率です。(④の導出)
$$I_D=\frac{b^3c}{3a\eta}\frac{eN_d}{\epsilon}\left(1-\frac{3}{b^2}\frac{2\epsilon}{eN_d}(\Delta\phi-V_G)+\frac{2}{b^3}\Big(\frac{2\epsilon}{eN_d}(\Delta\phi-V_G)\Big)^{3/2}\right) -④$$
ドレイン電流は、ゲートの負電圧を大きくすると、第1項と第2項により比例して大きくなりますが、さらにゲート電圧を大きくすると、第3項のることを表しますが、
②の導出
ドレイン電圧 $V(x)$ 、ドレイン電流 $I_D$ および抵抗 $R(x)$ の関係は、$x\sim x+dx$ について、
$$dV(x)=I_DdR(x) -(1)$$
この抵抗は、抵抗率を $\eta$ として、チャネルの幅を $2b-2W$ 、$z$ 軸方向の幅を $c$ であるから、
$$dR(x)=\frac{\eta dx}{2c\big(b-W(x)\big)} -(2)$$
(1) 、(2)と①より、
$$\eta I_Ddx=2c\left(b-\sqrt{\frac{2\epsilon}{eN_d}\big(\Delta\phi-V_G+V(x)\big)}\right)dV(x)$$
これをチャネルの全長に渡って積分すると②が導かれます。
$$\int_0^a\eta I_Ddx=2c\int_0^{V_D}\left(b-\sqrt{\frac{2\epsilon}{eN_d}\big(\Delta\phi-V_G+V(x)\big)}\right)dV(x)$$$$a\eta I_D=2c\left(bV_D-\frac{2}{3}\sqrt{\frac{2\epsilon}{eN_d}}\big((\Delta\phi-V_G+V_D)^{3/2}-(\Delta\phi-V_G)^{3/2}\big)\right)$$
④の導出
②で $V_D=V_p$ として③を代入すると④が得られます。
$$I_D=\frac{2c}{a\eta}\left(b\Big(\frac{eb^2N_d}{2\epsilon}-\Delta\phi+V_G\Big)-\frac{2}{3}\sqrt{\frac{2\epsilon}{eN_d}}\Big[\Big(\frac{eb^2N_d}{2\epsilon}\Big)^{3/2}-(\Delta\phi-V_G)^{3/2}\Big]\right)$$$$=\frac{2c}{a\eta}\left(\frac{1}{3}\frac{eb^3N_d}{2\epsilon}-b(\Delta\phi-V_G)+\frac{2}{3}\sqrt{\frac{2\epsilon}{eN_d}}(\Delta\phi-V_G)^{3/2}\right)$$$$=\frac{b^3c}{3a\eta}\frac{eN_d}{\epsilon}\left(1-\frac{3}{b^2}\frac{2\epsilon}{eN_d}(\Delta\phi-V_G)+\frac{2}{b^3}\Big(\frac{2\epsilon}{eN_d}\Big)^{3/2}(\Delta\phi-V_G)^{3/2}\right)$$
MOS型FET
MOS型FETのP型チャネルとN型チャネルの回路記号は以下になります。
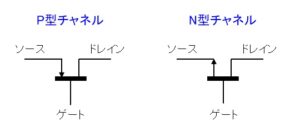
構造と仕組み
N型チャネルのMOS型FETの構造を以下に示します。P型チャネルの場合は、PNおよび電圧の極性入れ替えたものなります。N型チャネルのゲートは、P型半導体の表面に酸化物の絶縁膜を作り、その上に金属の電極を付着させています。
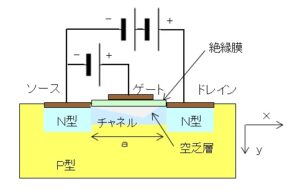
ゲート電極に正電圧を掛けると、P型半導体の表面にN型の反転層(チャネル)ができます。そして、ソースに負電圧、ドレインに正電圧が掛かるため、キャリヤ(電子)はソースからドレインに流れます(ドレイン電流)。
MOS型FETでは、ゲートに正電圧 $V_G$ によりN型チャネルが作られ、その電気伝導度を電界により制御することにより、ドレイン電流 $I_D$ を制御することができます。接合型FETと同様、ゲート電流はほとんど流れません。
また、ドレインの正電圧 $V_D$ と基板のP型半導体との間のPN接合は逆電圧になるため、空乏層ができます。ドレインの電圧を大きくすると、ドレイン側の空乏層の幅が大きくなり、ドレイン電流 $I_D$ を制御することができます。
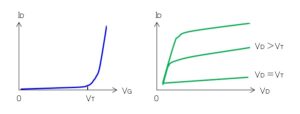
- ゲートの正電圧を上げるとチャネルの幅が大きくなり、ドレイン電流は増加する。ゲートの正電圧を下げるとチャネルの幅は小さくなり、ドレイン電流が減少する。
- ゲートの正電圧をさらに小さくするとチャネルがさらに狭くなり、チャネルは閉じられ(遮断電圧:$V_T$ )、この状態ではドレイン電流は遮断される。
- ドレイン電圧を大きくするとドレイン電流が増加するが、ドレイン側の空乏層が広がるため、ドレイン電流は飽和し一定となる(ピンチオフ)。
電流特性
MOS型FETの電流特性を導きます。ソースからドレインの方向に $x$ 軸、図の下方向に $y$ 軸をとり、空乏層の幅を $W$ 、チャネルの長さを $a$ 、$z$ 軸方向の幅を $c$ とします。ドレイン電流 $I_D$ とドレイン電圧 $V_D$ 、遮断電圧 $V_T$ の関係は以下で与えられます。(⑤の導出)
$$I_D=\frac{e\mu_nc}{a}\frac{\epsilon}{b}\Big((V_G-\Delta\phi)V_D-\frac{V_D^2}{2}\Big) -⑤$$
ここで $\mu_n$ は電子の移動率です。ピンチオフが起きたときの空乏層の幅は $W(x)=0$ となり、ドレイン電圧を $V(x)=V_p$(ピンチオフ電圧)とすると、飽和ドレイン電流は以下で得られます。(⑥の導出)
$$I_D=\frac{e\mu_n\epsilon c}{2ab}(V_G-V_T)^2 -⑥$$
⑤の導出
絶縁体をはさんでゲート電極側の正の表面電荷を $\sigma_g(x)$ 、チャネル中の負の面電荷を $\sigma_n(x)$ とすると、これらの大きさは等しくなるので、
$$\sigma_g(x)+\sigma_n(x)=0 -(3)$$
ゲート電圧を $V_G$ 、半導体の表面電位を $V_s$ 、絶縁層の厚さを $b$ とすると、ゲート電極の表面電荷はガウスの法則より、
$$\frac{\sigma_g(x)}{\epsilon}=E=\frac{V_G-V_s(x)}{b} -(4)$$
⑤の $\Delta\phi$ はゲート電圧が0の場合の障壁の高さであるので、
$$\Delta\phi=V_s(x)-V(x) -(5)$$
電子の移動度 $\mu$ と抵抗率 $\eta$ の関係 $\eta=1/ne\mu_n$ を使うと、チャネルの長さ $dx$ 当たりの電気抵抗 $dR$ は以下で表されます。
$$dR=\eta\frac{dx}{S}=-\frac{dx}{e\mu_nc\sigma_n(x)} -(6)$$
(4)を(3)に代入し(5)を使うと、
$$\sigma_n(x)=-\frac{\epsilon}{b}\big(V_G-V(x)-\Delta\phi\big) -(7)$$
(7)と(6)をオームの法則 $dV(x)=I_DdR(x)$ に代入すると、
$$\frac{I_D}{e\mu_nc}dx=\frac{\epsilon}{b}\big(V_G-V(x)-\Delta\phi\big)dV(x)$$
これをチャネルの全長に渡って積分すると⑤が導かれます。
$$\int_0^a\frac{I_D}{e\mu_nc}dx=\frac{\epsilon}{b}\int_0^{V_D}\big(V_G-V(x)-\Delta\phi\big)dV(x)$$$$\frac{aI_D}{e\mu_nc}=\frac{\epsilon}{b}\Big((V_G-\Delta\phi)V_D-\frac{V_D^2}{2}\Big)$$
⑥の導出
ピンチオフのときのドレイン電圧は、ドレイン側のチャネルの幅が0(チャネルの電荷が0)になるため、(7)より、
$$\sigma_n(x)=V_G-V_p-\Delta\phi=0 -(8)$$
⑤で $V_D=V_p$ 、$\Delta\phi=V_T$ とし、(8)を代入すると⑥が得られます。
$$I_D=\frac{e\mu_nc}{a}\frac{\epsilon}{b}\Big((V_G-V_T)^2-\frac{(V_G-V_T)^2}{2}\Big) \to⑤$$




