ラウエの条件
ラウエの条件とは、結晶格子による回折が起きる条件式です。この条件式は、散乱ベクトル $\Delta{\bf k}$ と逆格子ベクトル ${\bf G}$ により、以下で表されます。
$$\Delta{\bf k}={\bf G} -①$$
ここで、散乱ベクトルは入射波の波束ベクトル ${\bf k}$ と反射波の波束ベクトル ${\bf k’}$ により以下で定義されます。
$$\Delta{\bf k}\equiv{\bf k’}-{\bf k}$$$$|{\bf k}|=\frac{2\pi}{\lambda}$$
また、逆格子ベクトルは、結晶格子の基本並進ベクトル( ${\bf a},{\bf b},{\bf c}$ )から、以下で定義されます。尚、( $h,k,l$ )はミラー指数と呼ばれる整数です。
$${\bf G}\equiv h{\bf a}^*+k{\bf b}^*+l{\bf c}^*$$
$${\bf a}^*=\frac{{\bf b}\times{\bf c}}{{\bf a}\cdot({\bf b}\times{\bf c})}$$$${\bf b}^*=\frac{{\bf c}\times{\bf a}}{{\bf a}\cdot({\bf b}\times{\bf c})}$$$${\bf c}^*=\frac{{\bf a}\times{\bf b}}{{\bf a}\cdot({\bf b}\times{\bf c})}$$
回折条件を導く
以下、ラウエの条件を導きます。
位相差
最初に、互いに ${\bf r}$ 離れた体積素片 $dV$ で反射されるX線間の位相差を求めます。
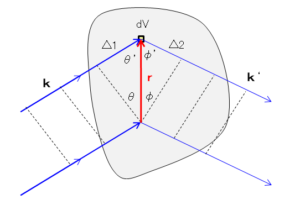
まず、入力X線の光路差は $\Delta_1=r\sin{\theta}$ であり、
$${\bf k}\cdot{\bf r}=kr\cos{(\pi/2-\theta)}=kr\sin{\theta}$$
であるため、位相差 $\theta_1$ は以下になります。
$$\theta_1=\frac{2\pi}{\lambda}\Delta_1=k\Delta_1={\bf k}\cdot{\bf r}$$
同様に、反射X線の光路差は、$\Delta_2=r\sin{\phi}$ であり、
$${\bf k’}\cdot{\bf r}=kr\cos{(\pi/2+\phi)}=-kr\sin{\phi}$$
であるため、位相差 $\theta_2$ は以下になります。
$$\theta_2=\frac{2\pi}{\lambda’}\Delta_2=k’\Delta_2=-{\bf k’}\cdot{\bf r}$$
従って、両方を合わせた位相差は、
$$\theta_1+\theta_2=({\bf k}-{\bf k’})\cdot{\bf r}=-\Delta{\bf k}\cdot{\bf r}$$
となります。これにより、位相因子 $e^{-i\Delta{\bf k}\cdot{\bf r}}$ が求められます。
散乱振幅
散乱振幅 $F$ とは、反射X線の強さを表す関数で、位相因子に電子密度 $n$ を掛けて積分することで求められます。
$$F=\int_Vn({\bf r})e^{-i\Delta{\bf k}\cdot{\bf r}}d{\bf r} -②$$
周期的な結晶構造内での電子密度は、逆格子ベクトルにより以下で表されるため、
$$n({\bf r})=\sum_Gn_Ge^{i{\bf G}\cdot{\bf r}}$$
これを②に代入すると以下になります。
$$F=\sum_G\int_Vn_Ge^{i({\bf G}-\Delta{\bf k})\cdot{\bf r}}d{\bf r}$$
従って、ラウエの条件①が成り立つときに位相因子は1になり、散乱振幅は次の極大値をもつことが分かります。
$$F=\sum_Gn_GV$$




