トンネル効果とは
トンネル効果(tunnelling effect)は、量子力学において、粒子がそのエネルギーよりも高いポテンシャルの壁を通り抜ける現象です。
左から右に運動するエネルギー $\epsilon$ の粒子が、幅 $a$ のポテンシャル $V(x)$ の壁に衝突する1次元の場合を考えます。
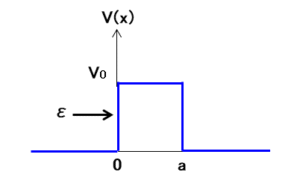
ポテンシャルを、
$$V(x)=\left\{\begin{array}{ll}
0 & (x\lt0\,,\,x\gt a) & -① \\
V_0 & (0\lt x\lt a) & -① \end{array} \right.$$
ポテンシャルの両側の波動関数を、$A\,,\,B\,,\,C$ を定数として以下の平面波で定義します。②の第1項は入力波、②の第2項は反射波、③は透過波を表します。
$$\left\{\begin{array}{ll}
\phi_1(x)\equiv Ae^{ikx}+Be^{-ikx} & (x\le0) & -② \\
\phi_2(x)\equiv Ce^{ikx} & (x\ge a) & -③ \end{array} \right.$$
この波動関数はシュレディンガー方程式に従うとします。
$$\Big(-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}+V(x)\Big)\phi(x)=\epsilon\phi(x) -④$$
このとき、入力波と反射波の2乗の比 $|B/A|^2$ 、および、入力波と透過波の2乗の比 $|C/A|^2$ は以下で表されます。
- $\epsilon\gt V_0$ の場合
$\alpha a=0\,,\,\pi\,,\,2\pi\,,\cdots,n\pi$ の場合に反射率⑤が $0$ 、透過率⑥が $1$ になります。また、⑤と⑥の和が常に $1$ になることはエネルギーの保存を表します。$$\Big|\frac{B}{A}\Big|^2=\Big(1+\frac{4\epsilon(\epsilon-V_0)}{V_0^2\sin^2{\kappa a}}\Big)^{-1} -⑤$$$$\Big|\frac{C}{A}\Big|^2=\Big(1+\frac{V_0^2\sin^2{\kappa a}}{4\epsilon(\epsilon-V_0)}\Big)^{-1} -⑥$$ - $\epsilon\lt V_0$ の場合
粒子のエネルギー $\epsilon$ が小さい場合、透過率⑦は極めて小さくなりますが、決してに $0$ はなりません。この現象をトンネル効果と呼びます。$$\Big|\frac{C}{A}\Big|^2=\Big(1+\frac{V_0^2\sinh^2{\alpha a}}{4\epsilon(V_0-\epsilon)}\Big)^{-1} -⑦$$
古典力学では $\epsilon\lt V_0$ の場合、粒子は $x\gt0$ の領域に侵入することはありませんが、量子論では、ポテンシャルの反対側にも粒子を見出すことができます。
トンネル効果を導く
④のシュレディンガー方程式は以下のように書き換えられます。
- $x\le 0$ と $x\ge a$ の場合:$V(x)=0$$$-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}\phi(x)=\epsilon\phi(x) -⑧$$$x\lt 0$ より平面波 $e^{ikx}$ を入力すると、$$\epsilon=\frac{\hbar^2k^2}{2m} -⑨$$
- $0\lt x\lt a$ の場合:$V(x)=V_0$$$\Big(-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}+V_0\Big)\phi(x)=\epsilon\phi(x) -⑩$$
境界条件
$x=0$ と $x=a$ において、波動関数とその微分は連続になる必要があります。$0\lt x\lt a$ での波動関数を $\phi_3(x)$ とすると、境界条件は以下で表されます。
-
- 境界条件1:$\phi_1(0)=\phi_3(0)$
- 境界条件2:$\phi’_1(0)=\phi’_3(0)$
- 境界条件3:$\phi_3(a)=\phi_2(a)$
- 境界条件4:$\phi’_3(a)=\phi’_2(a)$
$\epsilon\gt V_0$ の場合
$\alpha$ を以下のように定義し、⑨は以下のように書き換えます。
$$-\frac{d^2\phi}{dx^2}=\alpha^2\phi$$$$\alpha\equiv\sqrt{\frac{2m(\epsilon-V_0)}{\hbar^2}} -⑪$$
これを満たす波動関数 $\phi_3$ は以下で表されます。$D\,,\,E$ は定数です。
$$\phi_3(x)\equiv De^{i\alpha x}+Ee^{-i\alpha x}$$
各境界条件を適用すると、
- 境界条件1:$A+B=D+E$
- 境界条件2:$kA-kB=\alpha D-\alpha E$
- 境界条件3:$De^{i\alpha a}+Ee^{-i\alpha a}=Ce^{ika}$
- 境界条件4:$\alpha De^{i\alpha a}-\alpha Ee^{-i\alpha a}=kCe^{ika}$
境界条件1を境界条件2より $E$ を消去すると、
$$2\alpha D=(\alpha+k)A+(\alpha-k)B$$
これらを境界条件3に代入し $E$ と $D$ を消去し、$X\equiv B/A$ 、$Y\equiv C/A$ と置くと、
$$\Big((\alpha-k)e^{i\alpha a}+(\alpha+k)e^{-i\alpha a}\Big)X$$$$+(\alpha+k)e^{i\alpha a}+(\alpha-k)e^{-i\alpha a}=2\alpha Ye^{ika} -(1)$$
次に、境界条件4についても同様に計算すると、
$$\Big((\alpha-k)e^{i\alpha a}-(\alpha+k)e^{-i\alpha a}\Big)X$$$$+(\alpha+k)e^{i\alpha a}-(\alpha-k)e^{-i\alpha a}=2kYe^{ika} -(2)$$
(1)と(2)より $Ye^{ika}$ を消去すると、
$$k(\alpha+k)e^{i\alpha a}+k(\alpha-k)e^{-i\alpha a}+k\Big((\alpha-k)e^{i\alpha a}+(\alpha+k)e^{-i\alpha a}\Big)X$$$$=\alpha(\alpha+k)e^{i\alpha a}-\alpha(\alpha-k)e^{-i\alpha a}+\alpha\Big((\alpha-k)e^{i\alpha a}-(\alpha+k)e^{-i\alpha a}\Big)X$$$$X=\frac{(k^2-\alpha^2)(e^{-i\alpha a}-e^{i\alpha a})}{(k+\alpha)^2e^{-i\alpha a}-(k-\alpha)^2e^{i\alpha a}} -(3)$$
(3)を $X=(\xi+i\eta)/(\zeta+i\chi)$ の形に書き換え、$X$ の絶対値の2乗 $|X|^2=(\xi^2+\eta^2)/(\zeta^2+\chi^2)$ を求め、⑨と⑪を代入すると⑤が得られます。
$$|X|^2=\Big|\frac{B}{A}\Big|^2=\frac{(k^2-\alpha^2)\sin^2{\alpha a}}{4k^2\alpha^2+(k^2-\alpha^2)^2\sin^2{\alpha a}}$$$$=\Big(1+\frac{4\epsilon(\epsilon-V_0)}{V_0^2\sin^2{\alpha a}}\Big)^{-1} \to⑤$$
(3)を(1)に代入すると、
$$Y=\frac{4\alpha ke^{-i\alpha a}}{(k+\alpha)^2e^{-i\alpha a}-(k-\alpha)^2e^{i\alpha a}} -(4)$$
同様に、$Y$ の絶対値の2乗を求め、⑨と⑪を代入すると⑥が得られます。
$$|Y|^2=\Big|\frac{C}{A}\Big|^2=\frac{4k^2\alpha^2}{4k^2\alpha^2+(k^2-\alpha^2)^2\sin^2{\alpha a}}$$$$=\Big(1+\frac{V_0^2\sin^2{\alpha a}}{4\epsilon(\epsilon-V_0)}\Big)^{-1} \to⑥$$
$\epsilon\lt V_0$ の場合
$\beta$ を以下のように定義し、⑨は以下のように書き換えます。
$$\frac{d^2\phi}{dx^2}=\beta^2\phi$$$$\beta\equiv\sqrt{\frac{2m(V_0-\epsilon)}{\hbar^2}}$$
これを満たす波動関数 $\phi_3$ は以下で表されます。$D\,,\,E$ は定数です。
$$\phi_3(x)\equiv De^{\beta x}+Ee^{-\beta x}$$
各境界条件を適用すると、
- 境界条件1:$A+B=D+E$
- 境界条件2:$ikA-ikB=\beta D-\beta E$
- 境界条件3:$De^{\beta a}+Ee^{-\beta a}=Ce^{ika}$
- 境界条件4:$\beta De^{\beta a}-\beta Ee^{-\beta a}=ikCe^{ika}$
境界条件1を境界条件2より $E$ を消去すると、
$$2\beta D=(ik+\beta)A-(ik-\beta)B$$
これらを境界条件3に代入し $E$ と $D$ を消去し、$X\equiv B/A$ 、$Y\equiv C/A$ と置くと、
$$\Big(-(ik-\beta)e^{\beta a}+(ik+\beta)e^{-\beta a}\Big)X$$$$+(ik+\beta)e^{\beta a}-(ik-\beta)e^{-\beta a}=2\beta Ye^{ika} -(5)$$
次に、境界条件4についても同様に計算すると、
$$\Big(-(ik-\beta)e^{\beta a}-(ik+\beta)e^{-\beta a}\Big)X$$$$+(ik+\beta)e^{\beta a}+(ik-\beta)e^{-\beta a}=2ikYe^{ika} -(6)$$
(5)と(6)より $X$ を削除すると、
$$Y=\frac{4ik\beta e^{-ika}}{(ik+\beta)^2e^{-\beta x}-(ik-\beta)^2e^{\beta x}}$$
$Y$ の絶対値の2乗を求め、⑨と⑪を代入すると⑦が得られます。
$$|Y|^2=\Big|\frac{C}{A}\Big|^2=\frac{4k^2\beta^2}{4k^2\beta^2+(k^2+\beta^2)^2\sinh^2{\beta a}}$$$$=\Big(1+\frac{V_0^2\sinh^2{\beta a}}{4\epsilon(V_0-\epsilon)}\Big)^{-1} \to⑦$$




