ロンドン方程式
ロンドン方程式とは、超伝導の特徴の1つであるマイスナー効果の現象論的な解釈を与える方程式です。超伝導内の電流密度 ${\bf J}$ が磁場のベクトルポテンシャル ${\bf A}$ に比例すると仮定し以下のように表します。
$${\bf J}=-\frac{1}{\mu_0\lambda_L^2}{\bf A} -①$$
ここでは $\lambda_L$ はロンドンの侵入長と呼ばれ、以下で表されます(②の導出)。
$$\lambda_L=\sqrt{\frac{\epsilon_0mc^2}{nq^2}} -②$$
①の両辺の回転を取ると、$\nabla\times{\bf A}={\bf B}$ より、
$$\nabla\times{\bf J}=-\frac{1}{\mu_0\lambda_L^2}{\bf B} -③$$
②を導く
波動関数 $\psi$ と粒子数 $N$ に以下の関係があるとき、
$$\int_V\psi^*({\bf r})\psi({\bf r})d{\bf r}=N$$
$\psi$ は、質量密度 $n$ と位相 $\phi$ を用いて以下のように表されるとします。
$$\psi({\bf r})=\sqrt{n}e^{i\phi({\bf r})}$$$$\psi^*({\bf r})=\sqrt{n}e^{-i\phi({\bf r})}$$
磁場がある場合の運動量は ${\bf p}\,\to\,{\bf p}-q{\bf A}$ で表されるため、速度は、
$${\bf v}=\frac{1}{m}({\bf p}-q{\bf A})=\frac{1}{m}(-i\hbar\nabla-q{\bf A})$$
これより電流密度は、
$${\bf J}=\psi(q{\bf v})\psi^*=\frac{nq}{m}(\hbar\nabla\phi-q{\bf A})$$
両辺の回転を取り、$\epsilon_0\mu_0=1/c^2$ を使うと②が得られます。
$$\nabla\times{\bf J}=-\frac{nq^2}{m}\nabla\times{\bf A}=-\frac{1}{\mu_0}\Big(\frac{nq^2}{\epsilon_0mc^2}\Big){\bf B}$$
マイスナー効果
マイスナー効果とは、超伝導体を磁場の中で転移温度以下に冷却した場合、遮蔽電流(永久電流)の磁場が外部磁場を打ち消して、超伝導体内の磁束密度を0にする現象です。このとき、超伝導体内の磁場は以下の方程式で表されます(④を導く)。
$$\nabla^2{\bf B}=\frac{{\bf B}}{\lambda_L^2} -④$$
この場合、${\bf B}=0$ 以外の一定磁場は③の解にはなりません。$x$ 軸の正の側の空間を超伝導体が占めるとすると、
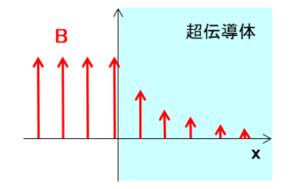
超伝導体内の磁場は以下で表されます。
$${\bf B}(x)={\bf B}_0e^{-x/\lambda_L}$$
④を導く
マクスウェル方程式より、
$$\nabla\times{\bf B}=\mu_0{\bf J}$$
この両辺に回転を取ると、
$$\nabla\times\nabla\times{\bf B}=\mu_0\nabla\times{\bf J}$$
この左辺は、
$$\nabla\times\nabla\times{\bf B}=\nabla(\nabla\cdot{\bf B})-\nabla^2{\bf B}=-\nabla^2{\bf B}$$
また右辺に③を使うと④が得られます。
$$-\nabla^2{\bf B}=\mu_0\nabla\times{\bf J}=-\frac{1}{\lambda_L^2}{\bf B}$$




