フラウンホーファ回折
フラウンホーファ回折とは、狭いスリットを通過した光が、十分離れた距離にあるスクリーン上で起こす回折現象です。
可視光の波長は $\sim10^{-7}m$ 程度なので、普段は回折は目立たず、光は直進するように見えますが、光源からの光を 0.1mm 程度以下の細いスリットに通すと、光は左右に回折して明暗の縞ができます。
光の強さを角度の関数 $I(\theta)$ で表すと、スリットの幅 $D$、光の波長 $\lambda$ より、以下のように表されます（①の導出）。
$$I(\theta)\propto\frac{\sin^2{\left(\frac{\pi D}{\lambda}\sin{\theta}\right)}}{\left(\frac{\pi D}{\lambda}\sin{\theta}\right)^2} -①$$
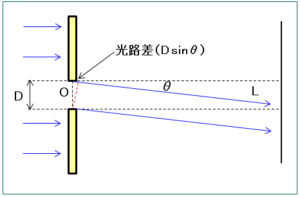
スリットの両端からの光路の差 $D\sin{\theta}$ が、光の波長の整数倍 $n$ になるような角度で、$I(\theta)=0$ となることが分かります。
$$D\sin{\theta}=n\lambda$$
式の導出
①の導出
スリットの中央 $O$（$x=0$）で発して、距離 $L$ に到達する光の振幅は以下で表されます。ここで、$A$ は比例定数です。
$$f(0)=A\sin{\Big(\frac{2\pi L}{\lambda}-\omega t\Big)}$$
$O$ から $x$ 離れた点から発した光は、上式の位相より $(2\pi/\lambda)x\sin{\theta}$ だけ遅れているので、
$$f(x)=A\sin{\Big(\frac{2\pi L}{\lambda}-\omega t-\frac{2\pi x}{\lambda}\sin{\theta}\Big)}$$
これをスリットの幅（$-D/2,D/2$）で積分すると、
$$F=A\int_{-D/2}^{D/2}\sin{\Big(\frac{2\pi L}{\lambda}-\omega t-\frac{2\pi x}{\lambda}\sin{\theta}\Big)}dx$$
$$=\frac{A\lambda}{2\pi\sin{\theta}}\left[\cos{\Big(\frac{2\pi L}{\lambda}-\omega t-\frac{2\pi x}{\lambda}\sin{\theta}\Big)}\right]_{-D/2}^{D/2}$$
三角関数の加法定理
$$\cos{(\alpha-\beta)}-\cos{(\alpha+\beta)}=2\sin{\alpha}\sin{\beta}$$
を使うと、
$$F=AD\frac{\lambda}{\pi D\sin{\theta}}\sin{\Big(\frac{2\pi L}{\lambda}-\omega t\Big)}\sin{\Big(\frac{\pi D}{\lambda}\sin{\theta}\Big)}$$
光の強さは振幅の２乗であるため、
$$I=F^2\propto\Big(\frac{\lambda}{\pi D\sin{\theta}}\Big)^2\sin^2{\Big(\frac{\pi D}{\lambda}\sin{\theta}\Big)}$$
これより①が得られることが分かります。
