熱力学第2法則は、熱の移動の不可逆性の法則です。別の表現をすれば、エントロピーの増大則とも言うことができます。
熱力学第2法則の話しの前に、カルノーサイクルについて説明します。
カルノーサイクル
カルノーサイクルには、熱機関とヒートポンプがあります。熱機関とは、外部から熱を受取り、外部に対して仕事を行う周期的なサイクルです。また、ヒートポンプとは、外部より仕事をされて、低温源から高温源に熱を移動させる周期的なサイクルです。例を挙げると、熱機関は蒸気機関であり、ヒートポンプはエアコンです。
以下に、可逆サイクルと不可逆サイクルを説明します。
可逆サイクル
可逆サイクル(可逆過程)とは、系の状態を $\alpha\to\alpha’$、外部の状態を $\beta\to\beta’$ と変化させた後に、なんらかの方法で、系の状態を $\alpha’\to\alpha$、外部の状態を $\beta’\to\beta$ と戻せる過程のことです。
以下の図は、左は熱機関、右はヒートポンプの表しています。熱機関は、高温源 $T1$ から低温源 $T2$ への熱の移動を利用し、外部に仕事 $W$ を行います。ヒートポンプは、仕事を与えることで、低温源から高温源に熱を移動させます。
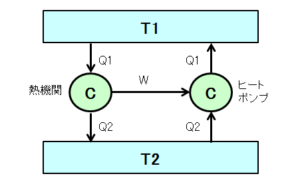
これらが可逆サイクルであれば、熱機関の行う仕事 $W$ によって、ヒートポンプは各熱源の状態を元に戻すことができます。熱力学第1法則は以下で表すことができます。
$$W=Q_1-Q_2$$
熱機関の熱効率 $\eta$ は、高温源からの熱と仕事の比で表すことができます。可逆サイクルの場合、この熱効率は両熱源の温度により表すことができます。つまり、可逆サイクルの熱効率は最大になります。
$$\eta\equiv\frac{W}{Q_1}=1-\frac{Q_2}{Q_1}=1-\frac{T_2}{T_1} -①$$
不可逆サイクル
不可逆サイクルの熱機関を図にすると以下になります。
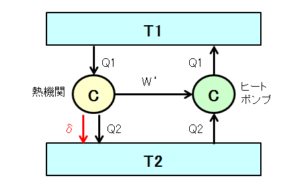
可逆サイクルとの違いは、摩擦熱 $\delta$ が発生してしまうことです。熱力学第1法則は以下になります。
$$W’=Q_1-Q_2-\delta$$
不可逆サイクルの熱効率 $\eta’$ は以下で表すことができます。
$$\eta’=\frac{W’}{Q_1}=1-\frac{Q_2+\delta}{Q_1}=1-\frac{Q’_2}{Q_1} -②$$
熱力学第2法則
熱力学第2法則には、いくつかの表現方法がありますが、これらは全て等価の内容を表しています。
クラジウスの不等式
摩擦熱は再利用ができません。不可逆サイクルの熱効率は、可逆サイクルの熱効率より小さくなります。
$$\eta’\lt\eta$$
①と②より、以下のクラジウスの不等式が導かれます。
$$\frac{Q_1}{T_1}-\frac{Q’_2}{T_2}\lt 0$$
熱 $Q$ の符号は、系に入る場合をプラス、系から出る場合をマイナスとすると、一般にクラジウスの不等式は以下で表すことができます。
$$\int\frac{\delta Q}{T}\lt 0$$
クラジウスの原理
クラジウスの原理とは、熱の移動の不可逆性を表しています。つまり、外部から何もしなければ、常に熱は温度が高い方から低い方に移動し、その逆は決して起こらないということです。
トムソンの原理
トムソンの原理とは、内部摩擦の不可逆性を表しています。つまり、ある物体から得た熱を全て仕事に変えられないことを表しています。熱効率が100%のサイクルを、第2種永久機関と呼ばれていますが、熱力学の第2法則は、第2種永久機関の存在を否定しています。
エントロピーの増大則
状態1から状態2に変化する場合のエントロピーの変化 $\Delta S$ は、以下で定義されます。
$$\Delta S\equiv\int_1^2\frac{\delta Q}{T}$$
これを微分を使って書くと以下になります。
$$dS=\frac{\delta Q}{T}$$
ここで、$P1$ から $P2$ が不可逆過程 $A$ で、$P2$ から $P1$ が可逆過程 $B$ であるサイクルを考えます。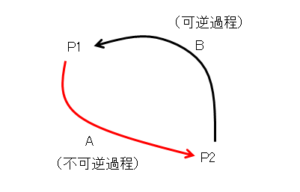
クラジウスの不等式より、以下が求められます。
$$0\gt\int\frac{\delta Q}{T}=\int_{1A2}\frac{\delta Q}{T}+\int_{2B1}\frac{\delta Q}{T}$$$$=\int_{1A2}\frac{\delta Q}{T}+S_1-S_2$$
熱の出入りがない孤立系($\delta Q=0$)の場合、以下の式になります。これは、$P1$ から $P2$ への不可逆過程で、常にエントロピーが増大していることを表しています。
$$S_2\gt S_1$$




