ストークスの定理とは
ストークスの定理とは、ベクトル場 $A$ の任意の曲面の周回積分が、そのベクトル場の回転(Rotation)の面積分に一致することを述べたものです。
$$\oint{\bf A}\cdot d{\bf s}=\int_S\nabla\times{\bf A}\cdot d{\bf S}$$
ここで、ナブラ記号は以下で定義されます。
$$\nabla\equiv\Big(\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z}\Big)$$
ストークスの定理を導く
任意の閉曲線の周回積分は、細分化した閉曲縁の周回積分の合計となります。イメージは以下の図になります。
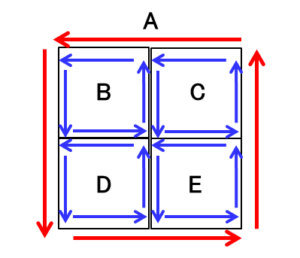
大きな四角Aを4つの四角B~Eに細分化します。各小さな四角の周回積分は、隣り合った同士の積分で打ち消し合いますので、小さな4つの四角の周回積分の合計は、元の四角Aの周回積分の値と等しくなります。そのため、任意の閉曲線を細分化した微小閉曲線で話しを進めます。
話しを簡単にするため、$xy$ 平面上にある一辺が $\Delta x$ と $\Delta y$ の微小領域を考えます。
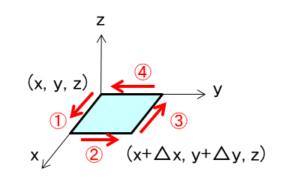
この微小領域の周囲を、①→②→③→④の順に積分を行います。
$$({\bf A}\cdot ds)_z=A_x(x,y,z)\Delta x+A_y(x+\Delta x,y,z)\Delta y$$$$-A_x(x,y+\Delta y,z)\Delta x-A_y(x,y,z)\Delta y$$
これを並べ替え、
$$({\bf A}\cdot ds)_z=\Big(A_y(x+\Delta x,y,z)-A_y(x,y,z)\Big)\Delta y$$$$-\Big(A_x(x,y+\Delta y,z)-A_x(x,y,z)\Big)\Delta x$$
微分形式で表すと
$$({\bf A}\cdot ds)_z=\Big(\frac{\partial A_y(x,y,z)}{\partial x}\Delta x\Big)\Delta y-\Big(\frac{\partial A_x(x,y,z)}{\partial y}\Delta y\Big)\Delta x$$
となるため、ベクトル積の使うと以下で表すことができます。
$$({\bf A}\cdot ds)_z=(\nabla\times{\bf A})_z\Delta x\Delta y$$
これより、ベクトル場の微小領域の周回積分は、ベクトル場の回転の面積分に置換えられることが分かります。そして、任意の面積分はその微小領域の面積分の和で求められるため、ストークスの定理が成り立つことが分かります。