ランダウ減衰とは
ランダウ減衰とは、衝突によるエネルギー散逸がないプラズマ中において、波動と粒子のエネルギー交換により発生する波の減衰です。
分散関係
ランダウ減衰の分散関係は以下で表されます。ここで $\omega_p$ はプラズマ振動数、$\lambda_D$ はデバイ長、$v_p$($=\omega/k$)は位相速度、$v_t$ は熱運動による速度です。
$$\omega=\omega_p\Big(1+i\frac{\pi}{2}\frac{\omega_p^2}{k^2}\frac{\partial\hat{f}_0}{\partial v}(v_p)\Big) -①$$$$\mathrm{Im}\Big(\frac{\omega}{\omega_p}\Big)=-ie^{-3/2}\sqrt{\pi}\Big(\frac{\omega_p}{kv_t}\Big)^3\exp{\Big(-\frac{1}{2k^2\lambda_D^2}\Big)} -②$$$$\omega_p^2\equiv\frac{n_0e^2}{\epsilon_0m}$$$$\lambda_D\equiv\sqrt{\frac{\epsilon_0k_BT}{n_0e^2}}$$$$\frac{1}{2}mv_t^2=k_BT$$
$\mathrm{Im}(\omega)$ が負なので、プラズマ波に減衰があることが分かります。この減衰は、$k\lambda_D\ll1$ の場合は小さくなりますが、$k\lambda_D\sim1$ の場合は影響が大きくなります。
尚、②の分散関係式は以下のマクスウェル分布を前提としています。ここで、$\hat{f}_0$ は粒子分布を表します。
$$\hat{f}_0=\sqrt{\frac{m}{2\pi k_BT}}e^{-mv^2/2k_BT}=\frac{1}{\sqrt{\pi}v_t}e^{-v^2/v_t^2} -③$$
減衰の仕組み
ランダウ減衰(分散関係の虚部)は、波の位相速度($v=v_p$)にある極から出てきており、位相速度にほとんど等しい速度をもつ粒子の存在が関連します。このことは、波乗りの仕組みからイメージすることができます。
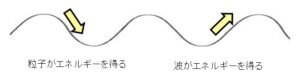
波(位相速度)が波乗り板(粒子)より少し速く動く場合、波が波乗り板を押すため、波がエネルギーを失い、波乗り板がエネルギーを得ます。逆に、波乗り板が波より少し速く動く場合、波乗り板が波を押すため、波乗り板がエネルギーを失い、波がエネルギーを得ます。
マクスウェル分布では速い粒子より遅い粒子が多いため、波にエネルギーを与える粒子より、波からエネルギーを奪う粒子が多く、全体として波は減衰します。
ランダウ減衰を導く
ランダウ減衰は無衝突の粒子の分布関数であるブラソフ方程式から導かれます。
$$\frac{\partial f}{\partial t}+{\bf v}\cdot\nabla f+\frac{q}{m}({\bf E}+{\bf v}\times{\bf B})\cdot\frac{\partial f}{\partial{\bf v}}=0$$
線形近似
以下のような線形近似を行うと、
$${\bf E}=(E_x,0,0) , E_x\propto e^{i(kx-\omega t)}$$$${\bf B}=0$$$$f({\bf r},{\bf v},t)=f_0({\bf v})+f_1({\bf r},{\bf v},t)$$$$f_1\propto e^{i(kx-\omega t)}$$
線形近似によりブラソフ方程式は以下になります。
$$-i\omega f_1+ikv_xf_1-\frac{eE_x}{m}\frac{\partial f_0}{\partial v_x}=0$$$$f_1=\frac{ieE_x}{m(\omega-kv_x)}\frac{\partial f_0}{\partial v_x} -④$$
同様にポアソン方程式(ガウスの法則)を書き変えると、
$$\nabla\cdot{\bf D}=\rho$$$$ikE_x=\frac{\rho}{\epsilon_0}=-\frac{en_1}{\epsilon_0}=-\frac{e}{\epsilon_0}\int f_1d^3v$$
これに④を代入し、$\hat{f}_0=f_0/n_0$ すると、
$$1=-\frac{e^2}{k\epsilon_0m}\int\frac{1}{\omega-kv_x}\frac{\partial f_0}{\partial v_x}d^3v$$$$=\frac{n_0e^2}{k^2\epsilon_0m}\int\frac{1}{v_x-\omega/k}\frac{\partial\hat{f}_0}{\partial v_x}d^3v$$
1次元のモデルとし($v_x\to v$)、プラズマ振動数を使うと、以下の分散関係式が得られます。
$$1=\frac{\omega_p^2}{k^2}\int_{-\infty}^\infty\frac{1}{v-v_p}\frac{\partial\hat{f}_0}{\partial v}dv -⑤$$
極周りの積分
⑤の積分は $v=v_p=\omega/k$ で極(特異点)を持ち、これがプラズマ波の分散関係に影響を与えるため、正しく取り扱う必要があります。通常は以下のような、下か上に半円形の積分路を用います。
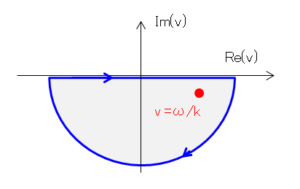
しかし、被積分関数のがマクスウェル分布の場合、$\hat{f}_0\propto e^{-v^2}$ であり $v\to\pm i\infty$ で積分は発散してしまいます。そのため、ランダウは次のような仮定に基づき、
- 減衰が弱い:$\mathrm{Im}(v_p)=\mathrm{Im}(\omega/k)\ll1$
- 位相速度が大きい:$|v_g|=|\omega/k|\gg1$
以下のような、極の周りに半円を持つ実軸上の積分路を設定しました。このとき、仮定1により極は実軸にすぐ下に存在します。
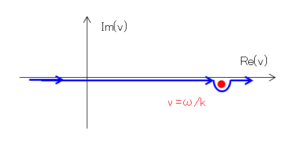
これにより、⑤の積分は実軸上の積分(第1項)と極の周りの積分(第2項)に分けられます。極の周りの積分は半周分であるため、コーシーの積分表示で得られる留数値 $2\pi i$ の半分の寄与になります。
$$1=\frac{\omega_p^2}{k^2}\Big(\int_{-\infty}^\infty\frac{1}{v-v_p}\frac{\partial\hat{f}_0}{\partial v}dv+i\pi\frac{\partial\hat{f}_0}{\partial v}(v_p)\Big)$$
右辺第1項については、仮定2より極付近の実軸上の積分からの寄与は小さくなります。部分積分で計算すると、
$$\int_{-\infty}^\infty\frac{1}{v-v_p}\frac{\partial\hat{f}_0}{\partial v}dv=\Big[\frac{\hat{f}_0}{v-v_p}\Big]_{-\infty}^\infty-\int_{-\infty}^\infty\frac{-\hat{f}_0}{(v-v_p)^2}dv$$$$=\int_{-\infty}^\infty\frac{\hat{f}_0}{(v-v_p)^2}dv$$
これより⑤は以下のように書き変えられます。
$$1=\frac{\omega_p^2}{k^2}\Big(\int_{-\infty}^\infty\frac{\hat{f}_0}{(v-v_p)^2}dv+i\pi\frac{\partial\hat{f}_0}{\partial v}(v_p)\Big) -⑥$$
分散関係①の導出
$v_p\gg v$ を仮定してテイラー展開すると、
$$\frac{1}{(v-v_p)^2}=\frac{1}{v_p^2}\Big(1-\frac{v}{v_p}\Big)^{-2}=\frac{1}{v_p^2}\Big(1+\frac{2v}{v_p}+\frac{3v^2}{v_p^2}+\cdots\Big) -⑦$$
⑥の第1項は(2)の左辺の平均であり、⑦の左辺の奇数項は平均することで消えるため、
$$\int_{-\infty}^\infty\frac{\hat{f}_0}{(v-v_p)^2}dv=\Big<\frac{1}{(v-v_p)^2}\Big>\cong\frac{1}{v_p^2}\Big(1+\frac{3}{v_p^2}\braket{v^2}\Big)$$$$=\frac{1}{v_p^2}\Big(1+\frac{3}{v_p^2}\frac{k_BT}{m}\Big)$$
ここで $\hat{f}_0$ をマクスウェル分布を仮定しています。
$$\frac{1}{2}m\braket{v^2}=\frac{1}{2}k_BT$$
⑥の両辺の実部を書き出し、$\omega\cong\omega_p$ のように近似をとると、
$$\omega^2=\omega_p^2+3k^2\frac{\omega_p^2}{\omega^2}\frac{k_BT}{m}\cong\omega_p^2+3k^2\frac{k_BT}{m}$$$$=\omega_p^2+\frac{3}{2}k^2v_t^2 -⑧$$
⑧の熱補正項(第2項)を無視すると、⑥は以下になります。
$$1=\frac{\omega_p^2}{\omega^2}+i\pi\frac{\omega_p^2}{k^2}\frac{\partial\hat{f}_0}{\partial v}(v_p)$$
これを $\omega$ について解きテイラー展開すると、①が得られます。
$$\omega=\omega_p\Big(1-i\pi\frac{\omega_p^2}{k^2}\frac{\partial\hat{f}_0}{\partial v}(v_p)\Big)^{-1/2}$$$$\cong\omega_p\Big(1+i\frac{\pi}{2}\frac{\omega_p^2}{k^2}\frac{\partial\hat{f}_0}{\partial v}(v_p)\Big) \to①$$
分散関係②の導出
マクスウェル分布を前提とし $\hat{f}_0$ を $v$ で微分すると、
$$\frac{\partial\hat{f}_0}{\partial v}=\frac{1}{\sqrt{\pi}v_t}\Big(-\frac{2v}{v_t^2}\Big)e^{-v^2/v_t^2}$$
これを①に代入し、$v=\omega/k$ とすると、
$$\omega=\omega_p\Big(1-i\frac{\sqrt{\pi}}{v_t^3}\frac{\omega_p^2}{k^2}\frac{\omega}{k}e^{-\omega^2/k^2v_t^2}\Big)$$
ここで第2項の係数で $\omega\cong\omega_p$ と近似し、指数部に⑧を代入すると②が得られます。
$$\mathrm{Im}\Big(\frac{\omega}{\omega_p}\Big)=-\sqrt{\pi}\Big(\frac{\omega_p}{kv_t}\Big)^3\exp{\Big(-\frac{\omega_p^2+\frac{3}{2}v_t^2k^2}{k^2v_t^2}\Big)}$$$$=-e^{-3/2}\sqrt{\pi}\Big(\frac{\omega_p}{kv_t}\Big)^3e^{-\omega_p^2/k^2v_t^2}$$$$=-e^{-3/2}\sqrt{\pi}\Big(\frac{\omega_p}{kv_t}\Big)^3\exp{\Big(-\frac{1}{2k^2\lambda_D^2}\Big)} \to②$$




