2資産での投資機会集合
投資機会集合とは、投資家が選択できるリターンとリスクの組み合わせです。複数の資産を上手く組み合わせることで、一定のリターンを確保しつつ、リスクを低減することが可能となります。
資産1と資産2のリスクを $\sigma_1$ と $\sigma_2$($\sigma_1\lt\sigma_2$)、資産1と資産2のリターンを $\mu_1$ と $\mu_2$($\mu_1\lt\mu_2$) とすると、2資産を組み合わせた場合のリターン $\mu$ とリスク $\sigma$ は以下で表されます。ここで、$w$ は資産1の全体に占める割合、$\rho$ は相関係数を表します。
$$\mu=w\mu_1+(1-w)\mu_2 -①$$
$$\sigma^2=w^2\sigma_1^2+2w(1-w)\sigma_1\sigma_2\rho+(1-w)^2\sigma_2^2 -②$$
この式の導出は以下の式を参照ください。
以下の3つのケースで投資機会集合を見てみますが、3資産以上の場合でも本質的に同じ傾向を持ちます。
順相関(ρ=1)の場合
順相関とは、2つの資産の価格が同じ方向に動く関係にあることです。$\rho=1$ のとき、リスク②は、
$$\sigma^2=\Big(w\sigma_1+(1-w)\sigma_2\Big)^2$$
右辺の括弧の中は常に正であるため、以下になります。
$$\sigma=w\sigma_1+(1-w)\sigma_2$$
従って、これにより①の $w$ を消去すると、リターンとリスクの関係は、
$$\mu=\frac{\mu_2-\mu_1}{\sigma_2-\sigma_1}\sigma+\frac{\mu_1\sigma_2-\mu_2\sigma_1}{\sigma_2-\sigma_1}$$
この式は、正の定数 $\alpha$、$\beta$ を使って以下のように書くことができます。
$$\mu=\alpha\sigma+\beta$$$$\alpha\equiv\frac{\mu_2-\mu_1}{\sigma_2-\sigma_1}$$$$\beta\equiv\frac{\mu_1\sigma_2-\mu_2\sigma_1}{\sigma_2-\sigma_1}$$
これを図で表すと以下になります。
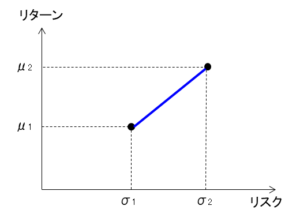
完全な順相関の場合、2資産のリターンとリスクの関係は、2つの資産を結ぶ直線で表すことができます。
逆相関(ρ=-1)の場合
逆相関とは、2つの資産の価格が逆の方向に動く関係にあることです。$\rho=-1$ のとき、リスク②は、
$$\sigma^2=\Big(w\sigma_1-(1-w)\sigma_2\Big)^2$$
この場合、右辺の括弧の中は、資産1の割合 $w$ が $\sigma_2/(\sigma_1+\sigma_2)$ より大きければ正、小さければ負となるので、これらを分けて書くと以下になります。
$$(1\ge w\ge w_c) \sigma=w\sigma_1-(1-w)\sigma_2$$$$(w_c\gt w\ge0) \sigma=-w\sigma_1+(1-w)\sigma_2$$$$w_c\equiv\frac{\sigma_2}{\sigma_1+\sigma_2}$$
従って、これにより①の $w$ を消去すると、リターンとリスクの関係は、
$$(1\ge w\ge w_c) \mu=-\frac{\mu_2-\mu_1}{\sigma_2+\sigma_1}\sigma+\frac{\mu_1\sigma_2+\mu_2\sigma_1}{\sigma_2+\sigma_1}$$$$(w_c\gt w\ge0) \mu=\frac{\mu_2-\mu_1}{\sigma_2+\sigma_1}\sigma+\frac{\mu_1\sigma_2+\mu_2\sigma_1}{\sigma_2+\sigma_1}$$
この式は、正の定数 $\alpha$、$\beta$ を使って以下のように書くことができます。
$$(1\ge w\ge w_c) \mu=-\alpha\sigma+\beta$$$$(w_c\gt w\ge0) \mu=\alpha\sigma+\beta$$$$\alpha\equiv\frac{\mu_2-\mu_1}{\sigma_2+\sigma_1}$$$$\beta\equiv\frac{\mu_1\sigma_2+\mu_2\sigma_1}{\sigma_2+\sigma_1}$$
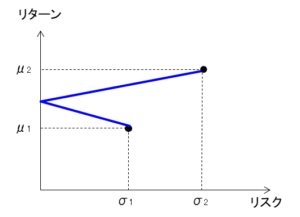
完全な逆相関の場合、$w=w_c$ でリスク $\sigma$ は0になり、直線のグラフは折れ曲がります。
無相関(ρ=0)の場合
無相関とは、2つの資産の価格の動きに関係が無いことです。$\rho=0$ のとき、リスク②は以下で表されます。
$$\sigma^2=w^2\sigma_1^2+(1-w)^2\sigma_2^2$$
従って、これにより①の $w$ を消去すると、リターンとリスクの関係は、
$$(\mu_2-\mu_1)^2\sigma^2=(\sigma_1^2+\sigma_2^2)\mu^2-2(\mu_2\sigma_1^2+\mu_1\sigma_2^2)\mu+\mu_2^2\sigma_1^2+\mu_1^2\sigma_2^2$$
この式は、正の定数 $\alpha$、$\beta$、$\gamma$ を使って以下のように書くことができます。
$$\sigma^2=\alpha\mu^2-2\beta\mu+\gamma$$
$$\alpha\equiv\frac{\sigma_1^2+\sigma_2^2}{(\mu_2-\mu_1)^2}$$$$\beta\equiv\frac{\mu_2\sigma_1^2+\mu_1\sigma_2^2}{(\mu_2-\mu_1)^2}$$$$\gamma\equiv\frac{\mu_2^2\sigma_1^2+\mu_1^2\sigma_2^2}{(\mu_2-\mu_1)^2}$$
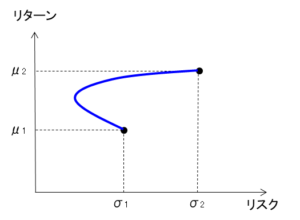
リスク $\sigma$ は0にはならず、グラフは曲線を描きます。




