シャノンの定理とは
シャノンの定理とは、誤りの生じる(雑音のある)通話路であっても、誤りのない情報の伝送速度を、通話路容量に近づけられることを示した定理です。
通話路の容量を $C$ 、情報伝達速度を $R$ とすると、任意に小さい誤り確率 $\epsilon$ で送れる符号化が存在することを示しています。
$$R=C-\epsilon (\epsilon\gt0)$$
シャノンの定理を導く
通信路の入力側につながれた情報源の1秒当たりのエントロピーを $H(X)$、送信信号の不確定度を表すエントロピーを $H_Y(X)$ とした場合、情報伝達速度 $R$ は以下で表されます。尚、$H_Y(X)$ は情報の「あいまい度」と呼ばれています。
$$R=H(X)-H_Y(X) -①$$
文字の種類が $k$ の場合のエントロピー(文字を表現するためのビット数)は、
$$H=\log_2{k}$$
文字数が $N$ の文字系列の総数は以下になります。
$$k^N=2^{HN}$$
従って①より、送信信号(入力)の文字列の総数は $2^{H(X)N}$ となります。この中から確実に送信できるのは、情報伝達速度分である $2^{RN}$ と考えることができるため、その確率は、
$$\frac{2^{RN}}{2^{H(X)N}}=2^{[R-H(X)]N}=2^{-H_Y(X)N} -②$$
その逆の確実に送信できない確率は以下で表されます。
$$1-2^{-H_Y(X)N} -③$$
1つの受信信号(下図赤点)に対する送信信号(文字数列)の候補の数は、情報のあいまい度 $H_Y(X)$ により $2^{H_Y(X)N}$(下図黄色)となります。尚、送信信号の総数は $2^{H(X)N}$ で、確実に送信できる数は $2^{RN}$(下図青点)です。
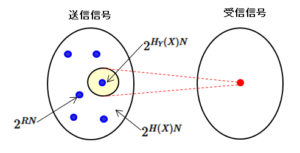
この $2^{H_Y(X)N}$(黄色)の中に1つだけ②の確率で現れる文字数列(青点)があればよいので、それ以外の文字数列( $2^{H_Y(X)N}-1$ )が確実に送信できない文字数列であるための確率 $P$ は、③により以下で表されます。
$$P=(1-2^{-H_Y(X)N})^{2^{H_Y(X)N}-1}$$
この確率 $P$ は、2つの異なる送信信号に対して、同じ受信信号が発生してしまう確率になります。ここで、十分に長い文字数列($N\gg1$)を仮定とすると、$2^{-H_Y(X)N}\ll1$ より、テイラー展開することができて、
$$P\cong 1-2^{-H_Y(X)N}(2^{H_Y(X)N}-1)\cong0$$
これにより文字数列を長く取ることにより、1つの送信信号に対し1つの受信信号を対応させることができる、つまり雑音による影響を限りなく小さくできることが分かります。




