量子位相推定
量子位相推定とは、ユニタリ演算子について、
$$U\ket{\phi}=e^{2\pi ij}\ket{\phi} -①$$
となる値 $j$（$0\le j\lt 1$）を求めることです。尚、$j$ を２進法で表すと、$j=0.j_1j_2\cdots j_n$ と表すことができます。
量子位相推定は、ユニタリ演算子 $U$ の固有関数 $\ket{\phi}$ と固有値 $e^{2\pi ij}$ の位相 $j$ を求める問題と言い換えることができます。
量子回路
量子位相推定を解くための量子回路は以下になります。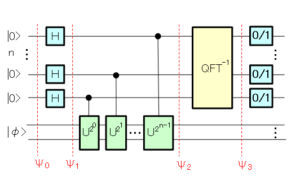
尚、［$H$］はアダマールゲート、［$U$］はユニタリゲートで、［$U^k$］はユニタリゲートを $k$ 回作用させることを表します。［$\mathrm{QFT}^{-1}$］は逆量子フーリエ変換です。
回路の上半分は $n$ ビットの制御ビットで、初期値は全て $\ket{0}$ です。この回路の入力状態は以下で表されます。
$$\Psi_0=\ket{0}\otimes\ket{0}\otimes\cdots\otimes\ket{0}\otimes\ket{\phi}$$
アダマールゲートを作用
アダマールゲートを作用させると、
$$\Psi_1=\frac{1}{\sqrt{2^n}}(\ket{0}+\ket{1})\otimes(\ket{0}+\ket{1})\otimes\cdots\otimes(\ket{0}+\ket{1})\otimes\ket{\phi} -②$$
ユニタリゲートを作用
次に、ユニタリゲートを作用させると、①より、
$$(\ket{0}+\ket{1})\otimes(U^{2^k}\ket{\phi})=(\ket{0}+\ket{1})\otimes(e^{2\pi ij2^k}\ket{\phi})$$$$=(\ket{0}+e^{2\pi ij2^k}\ket{1})\otimes\ket{\phi}$$
であるため、
$$\Psi_2=\frac{1}{\sqrt{2^n}}(\ket{0}+e^{2\pi ij2^{n-1}}\ket{1})\otimes(\ket{0}+e^{2\pi ij2^{n-2}}\ket{1})\otimes\cdots$$$$\cdots\otimes(\ket{0}+e^{2\pi ij2^0}\ket{1})\otimes\ket{\phi}$$
ここで、 $e^{2\pi im}=1$（$m$ は整数）を使うと、
$$e^{2\pi ij2^k}=e^{2\pi ij_1\cdots j_k(0.j_{k+1}\cdots j_n)}=e^{2\pi i(0.j_{k+1}\cdots j_n)}$$
従って、
$$\Psi_2=\frac{1}{\sqrt{2^n}}(\ket{0}+e^{2\pi i(0.j_n)}\ket{1})\otimes(\ket{0}+e^{2\pi i(0.j_{n-1}j_n)}\ket{1})\otimes\cdots$$$$\cdots\otimes(\ket{0}+e^{2\pi i(0.j_1\cdots j_n)}\ket{1})\otimes\ket{\phi} -③$$
逆量子フーリエ変換
③は量子フーリエ変換の出力になっており、③に逆量子フーリエ変換を作用させると、量子フーリエ変換の入力である以下を得ることができます。
$$\Psi_3=\ket{j_1j_2\cdots j_n}\otimes\ket{\phi}=\ket{j_1}\otimes\ket{j_2}\otimes\cdots\otimes\ket{j_n}\otimes\ket{\phi}$$
10進法での表記
②を書き換えると、
$$\Psi_1=\frac{1}{\sqrt{2^n}}(\ket{0\cdots00}+\ket{0\cdots01}+\cdots+\ket{1\cdots11})\otimes\ket{\phi}$$
これを10進法で表すと、
$$\Psi_1=\frac{1}{\sqrt{2^n}}(\ket{0}+\ket{1}+\cdots+\ket{2^n-1})\otimes\ket{\phi}$$$$=\frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^n-1}\ket{k}\otimes\ket{\phi}$$
ユニタリゲートを作用させると、以下のように表されます。
$$\Psi_2=\frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^n-1}\ket{k}\otimes(U^k\ket{\phi})$$$$=\frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^n-1}e^{2\pi ijk}\ket{k}\otimes\ket{\phi}$$
ここで $j=0.j_1j_2\cdots j_n$ であったため（但し、２進法表記）、$2^nj=J$ と置くと、
$$\Psi_2=\frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^n-1}e^{2\pi ikJ/2^n}\ket{k}\otimes\ket{\phi}$$
この上半分に対して逆量子フーリエ変換を行うことで、$J$ を求めることができます。
