波動方程式
波動方程式とは、音波や電磁波などの波動現象を記述するための方程式です。長さ $L$、線密度 $\rho$ の弦が、$x$ 軸方向に張力 $T$ で張られている弦の波動(振幅 $y$)を表す波動方程式は以下で表されます。
$$\frac{\partial^2y}{\partial x^2}=\frac{1}{c^2}\frac{\partial^2y}{\partial t^2} -①$$$$c=\sqrt{\frac{T}{\rho}}$$
波動方程式の導出
ニュートンの運動方程式 $F=ma$ を基に考えます。
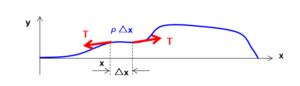
この右辺は、弦の素片の質量 $\rho\Delta x$ と、$y$ 軸方向の変位の加速度により、
$$ma=\rho\Delta x\frac{\partial^2y}{\partial t^2}$$
弦の素片に働く力は、その両端の張力の差になります。弦の方向と $y$ 軸のなす角度を $\theta$ とすると、$\sin{\theta}\cong\Delta y/\Delta x$ であり、$\Delta x\to0$ とすると、
$$F=T\sin{\theta’}-T\sin{\theta}$$$$\cong T\frac{\Delta y}{\Delta x}(x+\Delta x)-T\frac{\Delta y}{\Delta x}(x)$$$$\cong T\Delta x\frac{\partial^2y}{\partial x^2}$$
最後はテイラー展開を使いました。これらにより、ニュートン運動方程式は以下になります。
$$T\Delta x\frac{\partial^2y}{\partial x^2}=\rho\Delta x\frac{\partial^2y}{\partial t^2}$$
波の一般解
この波動方程式の一般解は以下で表されます。
$$y(x,t)=f(x-ct)+g(x+ct)$$$$=f(kx-\omega t)+g(kx+\omega t)$$
ここで、$v$ は波の速度(位相速度)、$\omega$ は角振動数、$k$ は波数、$\nu$ は振動数、$\lambda$ は波長です。それぞれの関係は以下になります。
$$c=\frac{\omega}{k}=\nu\lambda$$$$\omega=2\pi\nu$$$$k=\frac{2\pi}{\lambda}$$
境界条件
弦の両端が固定端の場合の境界条件は、
$$y(0,t)=y(L,t)=0$$
弦の振動は、固有振動の重ね合わせとして表すことができます。
$$y(x,t)=\sum_{n=1}^\infty A_n\sin{\frac{n\pi x}{L}}\sin{\Big(\frac{n\pi ct}{L}+\alpha_n\Big)}$$
導出
境界条件より、任意の波形は以下のフーリエ級数で表すことができます。
$$y(x)=\sum_{n=0}^\infty a_n\sin{\frac{n\pi x}{L}}$$
これを①に代入すると、
$$\frac{d^2a_n}{dt^2}+\Big(\frac{n\pi c}{L}\Big)^2a_n=0$$
これを解くと以下になります。
$$a_n=A_n\sin{\Big(\frac{n\pi ct}{L}+\alpha_n\Big)}$$
群速度
群速度とは、波の重ね合わせにより生じる「うねり」の速度です。波がエネルギーを運ぶ速度は群速度になります。角振動数と波数の近い2つの波を重ね合わせると、
$$y=A\Big(\sin{(\omega_1t-k_1x)}+\sin{(\omega_2t-k_2x)}\Big)$$$$=2A\sin{\Big(\frac{\omega_1+\omega_2}{2}t-\frac{k_1+k_2}{2}x\Big)}\cos{\Big(\frac{\omega_1-\omega_2}{2}t-\frac{k_1-k_2}{2}x\Big)} -②$$
これは波長の短い波($\omega_1+\omega_2$ と $k_1+k_2$)の振幅が、波長の長い波($\omega_1-\omega_2$ と $k_1-k_2$)の周期で振動しているように見えます。この長い波長の波を「うねり」と呼びます。このとき群速度(うねりの速度)は以下で表されます。
$$v=\frac{\omega_1-\omega_2}{k_1-k_2}=\frac{d\omega}{dk}$$
尚、②の計算は以下の公式を使いました。
$$\sin{(\alpha+\beta)}+\sin{(\alpha-\beta)}=2\sin{\alpha}\sin{\beta}$$
波のエネルギー
波のエネルギーとは、波を伝える媒体の運動エネルギーと変形による位置エネルギーです。振幅を $A$ 、質量を $m$ とすると、単振動のエネルギー $I$ は以下で表されるため、
$$I=\frac{m\omega^2A^2}{2}$$
単位面積を通過する波のエネルギーは、$m=\rho c$( $c$ は波の速度)より、以下で表されます。
$$I=\frac{\rho c\omega^2A^2}{2}$$




