決定木とは
決定木とは、分類や意思決定を多段階に繰り返して行う場合、その各段の分岐を階層的に樹形図で表したものです。
分岐の条件を入力変数 $x_i$ 、分岐の結果を目的変数 $t_j$ と呼びます。ここで、独立変数の数を $m$、独立変数のセット(データ)の数を $n$ とします。
$$t_j=t_j(x_1,x_2,\cdots,x_i,\cdots,x_m)$$$$j=1,2,\cdots,n$$
また、決定木の始点を根ノード、端点を葉ノードと呼びます。決定木が完成した状態では、1つの葉ノードに含まれるの全てのデータは同一の目的変数を持ちます。
この目的変数が数値型か分類型かにより、決定木は2つの種類に分かれます。
| 種類 | 目的変数 | 例 |
| 回帰木 | 数値型 | 価格の見積り、所要日数、飛距離など |
| 分類木 | 分類型 | 合格/不合格、勝ち/負け、実施/中止など |
以下の説明は、分類木に限定し、入力変数を「属性」、目的変数を「クラス」と呼ぶことにします。
学習アルゴリズム
決定木の学習アルゴリズムは以下になります。
- 根ノードに対し属性を選択し、子ノードに分岐させる
- その子ノードを親ノードとして、次の属性を選択し、子コードに分岐させる
- 全ての子ノードが葉ノードとなるまで 2. を繰り返す
決定木の根ノードでは、全てのデータ(全てのクラス)が含まれるため、最も多様性が大きくなりいます。また、葉ノードでは、そこに含まれるデータは全て同じクラスに属するため、最も多様性が小さくなります。
従って、分岐させる際に、多様性を最も下げる属性を選択することが、最も効率の良い学習アルゴリズムを作ることにつながります。決定木の学習アルゴリズムと、それに採用されている多様性の指数は以下になります。
| 学習アルゴリズム | 多様性指数 |
| CART(Classification and Regression Tree) | ジニ係数 |
| ID3(Iterative Dichotomiser 3) | 情報利得 |
| C4.5 / C5 | 情報利得比 |
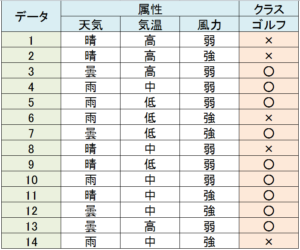
次のような、天候の条件によってゴルフの実施/中止を判断する例で、各多様性指数を計算してみます。
ゴルフ場の例
この例では、データの数 $n$ は14個、属性の数 $m$ は4個で、それぞれ天気(晴・曇・雨)、気温(高・中・低)、風力(強・弱)、クラスはゴルフの 「○:実施」または「 ×:中止」です。
ジニ係数
ジニ係数とは、経済の分野で所得格差を表すために使われていますが、多様性指標では、任意の2つのデータが異なるクラスに属する確率として解釈することができます。
ゴルフの例では、2つのデータを任意に選択して「○×」または「×○」の組み合わせになる確率がデータ集合の多様性を表すと考えます。「○」になる確率を $p_\circ$、「×」になる確率を $p_\times$ とすると($p_\circ+p_\times=1$)、ジニ係数 $G$ は以下で表されます。
$$G=1-(p_\circ^2+p_\times^2)=2p_\circ(1-p_\circ)$$
ジニ係数が小さければ多様性も小さくなり、ジニ係数を指標として効率的な決定木を構築することができます。
根ノードのジニ係数
根ノードのジニ係数 $G_0$ は、「○」は9個、「×」が5個であり、$p_\circ=9/14$、$p_\times=5/14$ であるため以下になります。
$$G_0=1-\Big(\frac{9^2}{14^2}+\frac{5^2}{14^2}\Big)\cong0.459$$
子ノードのジニ係数
天気・気温・風力で分岐された場合のジニ係数 $G_1$ は以下になります。
| 属性 | $p_\circ$ | $p_\times$ | $G_1$ | $G_0-G_1$ | ||
| 天気 | 晴 | 2/5 | 3/5 | 0.480 | 0.343 | 0.116 |
| 曇 | 4/4 | 0/4 | 0.000 | |||
| 雨 | 3/5 | 2/5 | 0.480 | |||
| 気温 | 高 | 2/4 | 2/4 | 0.500 | 0.440 | 0.019 |
| 中 | 4/6 | 2/6 | 0.444 | |||
| 低 | 3/4 | 1/4 | 0.375 | |||
| 風力 | 強 | 3/6 | 3/6 | 0.500 | 0.429 | 0.031 |
| 弱 | 6/8 | 2/8 | 0.375 | |||
例えば、天気を属性に選んだ場合、ジニ係数を計算すると、
- 晴:$G_{11}=1-\frac{2^2}{5^2}-\frac{3^2}{5^2}\cong0.480$
- 曇:$G_{12}=1-\frac{4^2}{4^2}-\frac{0^2}{4^2}=0$
- 雨:$G_{13}=1-\frac{3^2}{5^2}-\frac{2^2}{5^2}\cong0.480$
であり、晴・曇・雨は一定の確率で現れるため、全体のジニ係数はこの平均で求められるため、
$$G_1=\frac{5}{14}G_{11}+\frac{4}{14}G_{12}+\frac{5}{14}G_{13}\cong0.343$$$$G_0-G_1\cong0.116$$
同様に気温と風力を選んだ場合でジニ係数を計算すると、気温で分類した場合の多様性が最も小さくなる(最適な選択肢)であることが分かります。
情報利得
ID3の場合は多様性をエントロピー $H$ で表し、エントロピーの変化分が情報利得となります。エントロピーは、事象の発生確率 $p_i$ により以下で定義されます。
$$H=-\sum_ip_i\log_2{p_i}$$
分岐前のエントロピーを $H_0$ 、分岐後を $H_1$ とすると、情報利得 $I$ は以下で求められます。
$$I=H_0-H_1$$
この情報利得を最大にする属性を選択することで、効率的な決定木を構築することができます。
根ノードのエントロピー
ゴルフの例では、根ノードのエントロピー $H_0$ は、「○」は9個、「×」が5個であり、$p_\circ=9/14$、$p_\times=5/14$ であるため以下になります。
$$H_0=-\frac{9}{14}\log_2{\frac{9}{14}}-\frac{5}{14}\log_2{\frac{5}{14}}\cong0.940$$
子ノードのエントロピー
天気・気温・風力で分岐された場合のエントロピー $H_1$ は以下になります。
| 属性 | $p_\circ$ | $p_\times$ | $H_1$ | $H_0-H_1$ | ||
| 天気 | 晴 | 2/5 | 3/5 | 0.971 | 0.694 | 0.247 |
| 曇 | 4/4 | 0/4 | 0.000 | |||
| 雨 | 3/5 | 2/5 | 0.971 | |||
| 気温 | 高 | 2/4 | 2/4 | 1.000 | 0.911 | 0.029 |
| 中 | 4/6 | 2/6 | 0.918 | |||
| 低 | 3/4 | 1/4 | 0.811 | |||
| 風力 | 強 | 3/6 | 3/6 | 1.000 | 0.892 | 0.048 |
| 弱 | 6/8 | 2/8 | 0.811 | |||
例えば、天気を属性に選んだ場合、エントロピーを計算すると、
- 晴:$H_{11}=-\frac{2}{5}\log_2{\frac{2}{5}}-\frac{3}{5}\log_2{\frac{3}{5}}\cong0.971$
- 曇:$H_{12}=-\frac{4}{4}\log_2{\frac{4}{4}}-\frac{0}{4}\log_2{\frac{0}{4}}=0$
- 雨:$H_{13}=-\frac{3}{5}\log_2{\frac{3}{5}}-\frac{2}{5}\log_2{\frac{2}{5}}\cong0.971$
であり、晴・曇・雨は一定の確率で現れるため、全体のエントロピーはこの平均で求められるため、
$$H_1=\frac{5}{14}H_{11}+\frac{4}{14}H_{12}+\frac{5}{14}H_{13}\cong0.694$$$$I=H_0-H_1\cong0.247$$
同様に気温と風力を選んだ場合でエントロピーを計算すると、気温で分類した場合のエントロピーが最も小さい(情報利得が大きい)ことが分かります。




