ベルの不等式とは、量子力学において「隠れた変数」の存在を前提に導かれた関係式です。この不等式が成立しないことを実験(アスペの実験)で示されたことにより、量子力学では隠れた変数は存在しない、つまり量子力学で知りうる全ての情報が得られることが実証されました。
光子の偏光
ベルの不等式を説明するため、次の実験装置を考えます。Ca原子が励起状態から基底状態に戻るときに、2個の互いに直交した偏光をもつ光子を反対方向に放出することが知られており、これを利用します。
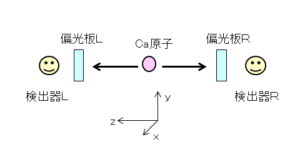
例えば、検出器Lでx軸方向の偏光が観測された場合、検出器Rではy軸方向の偏光が観測されます。言い方を代えると、偏光版Lをx軸に合わせたときに検出器Lで光子が観測された場合、検出器Rで光子が観測される確率は、偏光板をy軸に合わせた場合は1、x軸に合わせた場合は0、45°に傾けた場合は1/2になります。
ベルの不等式
偏光板Lの方向を $L_1$、偏光板Rの方向を $R_1$ に合わせ、検出器Lで光子が観測された場合に、検出器Rで光子が観測される確率を $P_{11}(L_1,R_1)$、逆に検出器Rで光子が観測されない確率を $P_{10}(L_1,R_1)$ などと表します。
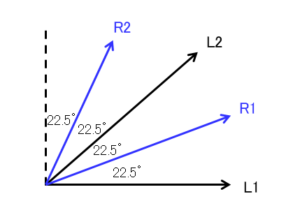
さらにそれぞれ偏光板の方向を $L_2$ と $R_2$ にも変え、偏光板の方向($L_1,L_2,R_1,R_2$)に対する、左と右で光子(偏光)が観測されるパターン($11,10,01,00$)の確率を考えます。ここで次の量Cを定義します。
$$C\equiv P(L_1,R_1)-P(L_1,R_2)+P(L_2,R_1)+P(L_2,R_2) -①$$
各項は以下のように計算されます。
$$P(L_1,R_1)=P_{11}(L_1,R_1)+P_{00}(L_1,R_1)-P_{10}(L_1,R_1)-P_{01}(L_1,R_1)$$$$P(L_1,R_2)=P_{11}(L_1,R_2)+P_{00}(L_1,R_2)-P_{10}(L_1,R_2)-P_{01}(L_1,R_2)$$$$P(L_2,R_1)=P_{11}(L_2,R_1)+P_{00}(L_2,R_1)-P_{10}(L_2,R_1)-P_{01}(L_2,R_1)$$$$P(L_2,R_2)=P_{11}(L_2,R_2)+P_{00}(L_2,R_2)-P_{10}(L_2,R_2)-P_{01}(L_2,R_2)$$
このとき、ベルの不等式は以下で表されます。
$$-2\le C\le2$$
実在論の場合
ある偏光板の組み合わせで測定を行ったとき、それ以外の偏光板の組合せが同時に観測されていれば、偏光の状態が1または0で得られていたはずだと仮定すると、次の16パターンが存在することになります。
| パターン | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| $L_1$ | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| $L_2$ | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| $R_1$ | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| $R_2$ | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
例えば、パターン1の場合で、①の16個の項を確率を計算すると以下になります。負号の項を赤字で表します。
| $P_{11}(L_1,R_1)=1$ | $P_{00}(L_1,R_1)=0$ | $P_{10}(L_1,R_1)=0$ | $P_{01}(L_1,R_1)=0$ |
| $P_{11}(L_1,R_2)=1$ | $P_{00}(L_1,R_2)=0$ | $P_{10}(L_1,R_2)=0$ | $P_{01}(L_1,R_2)=0$ |
| $P_{11}(L_2,R_1)=1$ | $P_{00}(L_2,R_1)=0$ | $P_{10}(L_2,R_1)=0$ | $P_{01}(L_2,R_1)=0$ |
| $P_{11}(L_2,R_2)=1$ | $P_{00}(L_2,R_2)=0$ | $P_{10}(L_2,R_2)=0$ | $P_{01}(L_2,R_2)=0$ |
従って以下のように、$C=2$ となりベルの不等式が成り立ちます。
$$C_1=(1+0-0-0)-(1+0-0-0)+(1+0-0-0)+(1+0-0-0)=2$$
その他のパターン2( $C_2$ )~パターン16( $C_{16}$ )を計算すると、以下のように全て $2$ または $-2$ の結果となります。
| $C_1=(1+0-0-0)-(1+0-0-0)+(1+0-0-0)+(1+0-0-0)=2$ $C_2=(0+0-0-1)-(0+0-0-1)+(1+0-0-0)+(1+0-0-0)=2$ $C_3=(1+0-0-0)-(1+0-0-0)+(0+0-0-1)+(0+0-0-1)=-2$ $C_4=(0+0-0-1)-(0+0-0-1)+(0+0-0-1)+(0+0-0-1)=-2$ $C_5=(0+0-1-0)-(1+0-0-0)+(0+0-1-0)+(1+0-0-0)=-2$ $C_6=(0+1-0-0)-(0+0-0-1)+(0+0-1-0)+(1+0-0-0)=2$ $C_7=(0+0-1-0)-(1+0-0-0)+(0+1-0-0)+(0+0-0-1)=-2$ $C_8=(0+1-0-0)-(0+0-0-1)+(0+1-0-0)+(0+0-0-1)=2$ $C_9=(1+0-0-0)-(0+0-1-0)+(1+0-0-0)+(0+0-1-0)=2$ $C_{10}=(0+0-0-1)-(0+1-0-0)+(1+0-0-0)+(0+0-1-0)=-2$ $C_{11}=(1+0-0-0)-(0+0-1-0)+(0+0-0-1)+(0+1-0-0)=2$ $C_{12}=(0+0-0-1)-(0+1-0-0)+(0+0-0-1)+(0+1-0-0)=-2$ $C_{13}=(0+0-1-0)-(0+0-1-0)+(0+0-1-0)+(0+0-1-0)=-2$ $C_{14}=(0+1-0-0)-(0+1-0-0)+(0+0-1-0)+(0+0-1-0)=-2$ $C_{15}=(0+0-1-0)-(0+0-1-0)+(0+1-0-0)+(0+1-0-0)=2$ $C_{16}=(0+1-0-0)-(0+1-0-0)+(0+1-0-0)+(0+1-0-0)=2$ |
実際は、パターン1からパターン16が混在しますから、①の値はベルの不等式の範囲内の値を取ります。
量子論の場合
90°角を4等分して、L1~R1、R1~L2、L2~R2がそれぞれ22.5°になるように設定します。このとき、①の第2項(負符号部分)のみ、角度が67.5°(=90°-22.5°)となっていることに留意してください。
この条件で、①の項を計算します。量子論の場合は、観測されない間は光子の偏光は確定せず、どちらか片方の光子が観測された時点で初めて、双方の偏光が確定すると考えます。
まず、$P_{11}(L_1,R_1)$ ですが、左側で光子が観測されたということは、左側の光子の偏光は $L_1$ と平行であるため、右側の光子の偏光はそれと直角($R_1$ に対し67.5°)になります。この光子が $R_1$ を通過する確率を考慮すると、
$$P_{11}(L_1,R_1)=\frac{1}{2}\cos^2(67.5°)\cong 0.073$$
ここで、右辺の1/2は左側の光子が偏光板を通過する確率です。尚、左の光子が先に観測された前提の説明をしていますが、実際は左右の観測される順番は関係ありません。
次に、例えば $P_{10}(L_1,R_1)$ ですが、左側で光子が観測されたということは、先ほど同様、右側の光子の偏光は $R_1$ に対し67.5°になります。今度は、この光子が $R_1$ を通過”しない”確率なので、
$$P_{10}(L_1,R_1)=\frac{1}{2}\cos^2(22.5°)\cong 0.427$$
このようして、①の16個の項を計算すると、
| $P_{11}(L_1,R_1) \cong 0.073$ | $P_{00}(L_1,R_1) \cong 0.073$ | $P_{10}(L_1,R_1) \cong 0.427$ | $P_{01}(L_1,R_1) \cong 0.427$ |
| $P_{11}(L_1,R_2) \cong 0.427$ | $P_{00}(L_1,R_2) \cong 0.427$ | $P_{10}(L_1,R_2) \cong 0.073$ | $P_{01}(L_1,R_2) \cong 0.073$ |
| $P_{11}(L_2,R_1) \cong 0.073$ | $P_{00}(L_2,R_1) \cong 0.073$ | $P_{10}(L_2,R_1) \cong 0.427$ | $P_{01}(L_2,R_1) \cong 0.427$ |
| $P_{11}(L_2,R_2) \cong 0.073$ | $P_{00}(L_2,R_2) \cong 0.073$ | $P_{10}(L_2,R_2) \cong 0.427$ | $P_{01}(L_2,R_2) \cong 0.427$ |
従って、
$$C=(0.073+0.073-0.427-0.427)-(0.427+0.427-0.073-0.073)$$$$+(0.073+0.073-0.427-0.427)+(0.073+0.073-0.427-0.427)$$$$\cong -2.828\lt -2$$
となり、量子論を前提とすると、ベルの不等式が成り立たないことが分かります。
尚、①の第1項中の4つの項のうち2つに負符号が付いていますが、これを正符号にすると①の第1項は”1”になります。
左右で偏光板を通過する/しないの4通りなので、全ての和が1になるのは当然のことです。これは、実在論であろうと、量子論であろうと変わりません。要所に負符号を入れたことは、ベルの不等式の妙と言えます。




