ナッシュ交渉解
ナッシュの交渉解とは、2人の交渉ゲーム(協力ゲーム)において、交渉の妥協点がもつ性質(公理)のことで、以下の4つが挙げられています。この4つの公理を満たす妥協点(交渉解)は、ただ1つ存在することがナッシュにより示されました。
- パレート最適性
- 対称性
- 利得の尺度や原点からの独立性
- 無関係な結果からの独立性
交渉の出発点は基準点と呼ばれます。以下、プレイヤ1とプレイヤ2の利得を( $u_1,u_2$ )、それぞれの基準点を( $u_1^0,u_2^0$ )で表します。また、互いが取りうる利得の範囲は実現可能領域 $R$ と呼ばれています。
ナッシュの交渉解( $u_1^*,u_2^*$ )は、基準点の組 $u^0$ と実現可能領域 $R$ から、以下の関数 $f$ を最大にする条件として得ることができます。
$$f(R,u^0)=\mathrm{max}\Big[(u_1-u_1^0)(u_2-u_2^0)\Big] -①$$
公理1.パレート最適性
パレート最適とは、交渉の妥協点において、あるプレイヤの利得を上げようとすると、他のプレイヤの利得が下がる状態を指します。つまり、パレート最適の状態は、全てのプレイヤの利得を上げる交渉解が存在しない状態です。
ナッシュの交渉解( $u_1^*,u_2^*$ )がパレート最適であるとは、その他の全ての交渉解( $u_1,u_2$ )$\in R$ について、以下の関係が成り立つことをいいます。
$$f^*(R,u^0)=(u_1^*-u_1^0)(u_2^*-u_2^0)\ge(u_1-u_1^0)(u_2-u_2^0) -②$$
公理1の証明
$u’_1\ge u_1^*$ と $u’_2\ge u_2^*$ を同時に満たす交渉解( $u’_1,u’_2$ )が存在すると仮定すると、
$$f’\equiv(u’_1-u_1^0)(u’_2-u_2^0)\ge(u_1^*-u_1^0)(u_2^*-u_2^0)=f^*$$
となってしまうため、ナッシュの交渉解( $u_1^*,u_2^*$ )のときに最大値 $f^*$ を取るという前提に矛盾します。従って、パレート最適の状態では、全てのプレイヤの利得を上げる交渉解が存在しないことが分かります。
公理2.対称性
対称性とは、基準点における2人のプレイヤの利得が等しく、かつ、実現可能領域がプレイヤの立場を変えても変わらない場合、交渉の妥協点での2人のプレイヤの同じ利得を得るというものです。次の利得表の場合を考えます。
| $(u_1,u_2)$ | $u_2(X)$ | $u_2(Y)$ |
| $u_1(X)$ | $(5,3)$ | $(0,0)$ |
| $u_1(Y)$ | $(0,0)$ | $(3,5)$ |
この利得表を図で表すと以下になります。横軸がプレイヤ1の利得、縦軸がプレイヤ2の利得を表します。純粋戦略の場合は取りうる利得は(5、3)、(3、5)、(0、0)の3つですが、相関戦略まで含めた実現可能領域は青色の三角形で表すことができます。
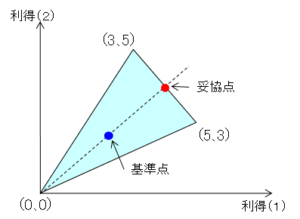
ナッシュの交渉解( $u_1^*,u_2^*$ )が対象であるとは、以下の関係が成り立つことを意味します。
$$u_1^*=u_2^* -③$$
公理2の証明
$u_1^0=u_2^0\equiv u^0$ のときに $u_1^*\ne u_2^*$ であると仮定し、$u’_1=u’_2\equiv(u_1^*+u_2^*)/2$ とすると、
$$f’=(u’_1-u_1^0)(u’_2-u_2^0)=\Big(\frac{u_1^*+u_2^*}{2}-u^0\Big)\Big(\frac{u_1^*+u_2^*}{2}-u^0\Big)$$$$=\frac{1}{4}\Big((u_1^*-u^0)^2+(u_2^*-u^0)^2+2(u_1^*-u^0)(u_2^*-u^0)\Big)$$$$\gt\frac{1}{4}\Big(2(u_1^*-u^0)(u_2^*-u^0)+2(u_1^*-u^0)(u_2^*-u^0)\Big)$$$$=(u_1^*-u^0)(u_2^*-u^0)= f^*$$
となってしまうため、ナッシュの交渉解( $u_1^*,u_2^*$ )のときに最大値 $f^*$ を取るという前提に矛盾します。従って、交渉の妥協点では、2人のプレイヤが同じ利得を得ることが分かります。尚、途中の不等式は、$a\ne b$ の場合に以下の不等式が成り立つことを使っています。
$$a^2+b^2\gt 2ab$$
公理3.利得の尺度や原点からの独立性
ナッシュの交渉解は、利得の尺度や原点を変わってもその妥協点は変わりません。例えば、上の利得表でプレイヤ1の利得を2倍して、プレイヤ2の利得に5を足した場合、現可能領域の三角形の位置や形は変わりますが、妥協点は変わらないことを表しています。
| $(u_1,u_2)$ | $u_2(X)$ | $u_2(Y)$ |
| $u_1(X)$ | $(10,8)$ | $(0,5)$ |
| $u_1(Y)$ | $(0,5)$ | $(6,10)$ |
利得の尺度や原点の変換( $u_1,u_2$ )$\to$( $v_1,v_2$ )を以下で表すと、
$$v_1=\alpha_1u_1+\beta_1 -④$$$$v_2=\alpha_2u_2+\beta_2 -④$$
変換後のナッシュの交渉解が以下で表されることを意味します。
$$v_1^*=\alpha_1u_1^*+\beta_1$$$$v_2^*=\alpha_2u_2^*+\beta_2$$
公理3の証明
④の変換式を使うと、新しい実現可能領域での交渉解 $g$ は以下になるため、
$$g=(v_1-v_1^0)(v_2-v_2^0)$$$$=\Big(\alpha_1u_1+\beta_1-(\alpha_1u_1^0+\beta_1)\Big)\Big(\alpha_2u_2+\beta_2-(\alpha_2u_2^0+\beta_2)\Big)$$$$=\alpha_1\alpha_2(u_1-u_1^0)(u_2-u_2^0)$$
$v’_1\ne v_1^*$ 、$v’_2\ne v_2^*$ となる( $v’_1,v’_2$ )が妥協解( $g’\gt g^*$)であると仮定すると、
$$g’=(v’_1-v_1^0)(v’_2-v_2^0)\gt(v_1^*-v_1^0)(v_2^*-v_2^0)=g^*$$$$\alpha_1\alpha_2(u’_1-u_1^0)(u’_2-u_2^0)\gt\alpha_1\alpha_2(u_1^*-u_1^0)(u_2^*-u_2^0)$$$$f’\gt f^*$$
となってしまうため、ナッシュの交渉解( $u_1^*,u_2^*$ )のときに最大値 $f^*$ を取るという前提に矛盾します。従って、利得の尺度や原点を変わってもその妥協点は変わらないことが分かります。
公理4.無関係な結果からの独立性
無関係な結果からの独立性とは、交渉の基準点と妥協点以外の領域が実現可能領域から取り除かれたとしても、交渉の基準点が変わらなければ妥協点も変わらないことを指します。
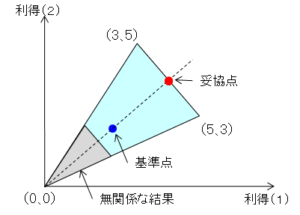
例えば、基準点と妥協点以外の部分(上図の灰色部分)を取り除いても、妥協点には影響がないことを意味します。
唯一性の導出
4つの公理が成り立つとき、妥協点( $u_1^*,u_2^*$ )はただ1つ存在することを導きます。公理3の変換を以下で定義し、公理2の対称性を使うと、
$$v_1\equiv\frac{u_1-u_1^0}{2(u_1^*-u_1^0)}=\frac{u_1-u^0}{2(u^*-u^0)}$$$$v_2\equiv\frac{u_2-u_2^0}{2(u_2^*-u_2^0)}=\frac{u_2-u^0}{2(u^*-u^0)}$$
変換後の基準点は( $0,0$ )、妥協点は( $1/2,1/2$ )、$g^*=1/4$ となります。ここで公理1を考慮し、$g’\le g^*$ となる妥協点( $v’_1,v’_2$ )が存在したとすると、
$$\frac{1}{4}\ge g’=v’_1v’_2=\frac{(u’_1-u^0)(u’_2-u^0)}{4(u^*-u^0)^2}$$$$(u^*-u^0)^2\ge(u’_1-u^0)(u’_2-u^0)$$
この等号が成り立つのは唯一 $u’_1=u’_2=u^*$ の場合であることが分かります。




