ローラン展開とは
ローラン展開(ローラン級数)とは、負のべき数にも拡張した級数展開で、テイラー展開との違いは以下が挙げられます。
- 複素関数の表示が可能
- 不正則(微分不可)な点を中心とした展開が可能
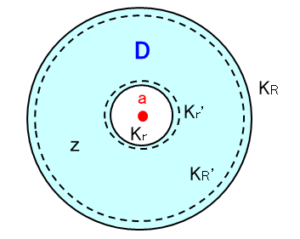
$z=x+iy$ として、$f(z)$ が円環領域 $D:0\le r\lt|z-a|\lt R\le\infty$ において正則(微分可能)でならば、以下の級数で一意的に展開されます。ここで、$K_\rho$ は $a$ を中心に半径 $\rho$($r\lt\rho\lt R$)の円周を表します。
$$f(z)=\sum_{n=-\infty}^\infty b_n(z-a)^n -①$$$$b_n\equiv\frac{1}{2\pi i}\int_{K_\rho}\frac{f(\zeta)}{(\zeta-a)^{n+1}}d\zeta$$
ローラン展開を導く
$r’$ と $R’$ を $r\lt r’\lt|z-a|\lt R’\lt R\le$ となるように定めると、$f(z)$ はコーシーの積分表示により以下で表されます。
$$f(z)=\frac{1}{2\pi i}\int_{K_{R’}}\frac{f(\zeta)}{\zeta-z}d\zeta-\frac{1}{2\pi i}\int_{K_{r’}}\frac{f(\zeta)}{\zeta-z}d\zeta -②$$
以下で求められる③と④を②に代入すると①が得られます。
$$f(z)=\sum_{n=0}^\infty b_n(z-a)^n+\sum_{m=-1}^\infty b_m(z-a)^m \to①$$
②の第1項の計算
$\zeta\in K_{R’}$ なので、
$$\Big|\frac{z-a}{\zeta-a}\Big|=\frac{|z-a|}{R’}\lt1$$
②の第1項の分母を計算すると、
$$\frac{1}{\zeta-z}=\frac{1}{\zeta-a}\cdot\frac{1}{1-\frac{z-a}{\zeta-a}}=\frac{1}{\zeta-a}\sum_{n=0}^\infty\Big(\frac{z-a}{\zeta-a}\Big)^n$$
これを②の第1項に代入します。一様収束する級数は個別に積分できるため、
$$\frac{1}{2\pi i}\int_{K_{R’}}\frac{f(\zeta)}{\zeta-z}d\zeta=\frac{1}{2\pi i}\int_{K_{R’}}f(\zeta)\sum_{n=0}^\infty\frac{(z-a)^n}{(\zeta-a)^{n+1}}d\zeta$$$$=\sum_{n=0}^\infty(z-a)^n\Big(\frac{1}{2\pi i}\int_{K_{R’}}\frac{f(\zeta)}{(\zeta-a)^{n+1}}d\zeta\Big)$$$$=\sum_{n=0}^\infty b_n(z-a)^n -③$$
被積分関数は、円環領域 $D$ で正則であることから、$K_{R’}$ と $K_\rho$ の積分の値が等しくなるため、$b_n$ で書き換えることができます。
①の第2項の計算
$\zeta\in K_{r’}$ なので、
$$\Big|\frac{\zeta-a}{z-a}\Big|=\frac{r’}{|z-a|}\lt1$$
②の第2項の分母を計算すると、
$$\frac{1}{\zeta-z}=-\frac{1}{z-a}\cdot\frac{1}{1-\frac{\zeta-a}{z-a}}=-\frac{1}{z-a}\sum_{m=0}^\infty\Big(\frac{\zeta-a}{z-a}\Big)^m$$
これを②の第2項に代入します。一様収束する級数は個別に積分できるため、
$$-\frac{1}{2\pi i}\int_{K_{r’}}\frac{f(\zeta)}{\zeta-z}d\zeta=\frac{1}{2\pi i}\int_{K_{r’}}f(\zeta)\sum_{m=1}^\infty\frac{(\zeta-a)^{m-1}}{(z-a)^m}d\zeta$$$$=\sum_{m=1}^\infty\frac{1}{(z-a)^m}\Big(\frac{1}{2\pi i}\int_{K_{r’}}f(\zeta)(\zeta-a)^{m-1}d\zeta\Big)$$$$=\sum_{m=1}^\infty\frac{b_{-m}}{(z-a)^m}=\sum_{m=-1}^\infty b_m(z-a)^m -④$$
被積分関数は、円環領域 $D$ で正則であることから、$K_{r’}$ と $K_\rho$ の積分の値が等しくなるため、$b_m$ で書き換えることができます。




