チェバの定理
チェバの定理とは、三角形の3つの頂点から対辺(またはその延長上)に引いた3本の線分が1点で交わるための条件を示す定理です。また、このような線分は共点と呼ばれます。
三角形の各頂点 $A,B,C$ と3つの対辺 $BC,CA,AB$ またはその延長上の点 $P,Q,R$ を通る直線が点 $O$ を通る場合、以下の関係が成り立ちます。
$$\frac{BP}{PC}\cdot\frac{CQ}{QA}\cdot\frac{AR}{RB}=1 -①$$
逆に、①の関係が成り立つ場合、線分 $AP,BQ,CR$ は一点で交わるか、全て平行になります。
①の導出
$A$ を通って $BC$ に平行に引いた直線と、$BQ,CR$ との交点を $D,E$ とします。
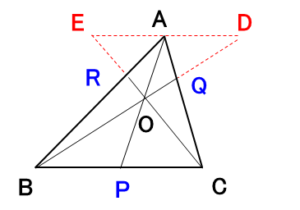
このとき以下の関係が成り立ちます。
$$\frac{BP}{DA}=\frac{PO}{AO}=\frac{PC}{AE}$$
このとき、
$$\frac{BP}{PC}=\frac{DA}{AE}$$
また、点 $Q$ と $R$ について、
$$\frac{CQ}{QA}=\frac{CB}{DA}$$$$\frac{AR}{RB}=\frac{AE}{CB}$$
これらより①が得られます。
$$\frac{BP}{PC}\cdot\frac{CQ}{QA}\cdot\frac{AR}{RB}=\frac{DA}{AE}\cdot\frac{CB}{DA}\cdot\frac{AE}{CB}=1$$
内角による表現
三角形の各頂点 $A,B,C$ と3つの対辺 $BC,CA,AB$ またはその延長上の点 $P,Q,R$ を通る直線が点 $O$ を通る場合、以下の関係が成り立ちます。
$$\frac{\sin{\angle BAP}}{\sin{\angle PAC}}\cdot\frac{\sin{\angle CBQ}}{\sin{\angle QBA}}\cdot\frac{\sin{\angle ACR}}{\sin{\angle RCB}}=1 -②$$
逆に、②の関係が成り立つ場合、線分 $AP,BQ,CR$ は一点で交わるか、全て平行になります。
②の導出
まず頂点 $A$ に着目し、点 $B,C$ から線分 $AP$ に垂直に下した点をそれぞれ $D,E$ とします。
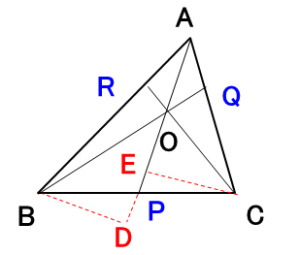
このとき線分とは平行であるため、以下の関係が成り立ちます。
$$\frac{AB\sin{\angle BAP}}{AC\sin{\angle PAC}}=\frac{BD}{CE}=\frac{BP}{PC}$$
次に頂点に $B$ と $C$ については、
$$\frac{BC\sin{\angle CBQ}}{AB\sin{\angle QBA}}=\frac{CQ}{QA}$$$$\frac{AC\sin{\angle ACR}}{BC\sin{\angle RCB}}=\frac{AR}{RB}$$
これらより①を使うと②が得られます。
$$\frac{\sin{\angle BAP}}{\sin{\angle PAC}}\cdot\frac{\sin{\angle CBQ}}{\sin{\angle QBA}}\cdot\frac{\sin{\angle ACR}}{\sin{\angle RCB}}=\frac{BP}{PC}\cdot\frac{CQ}{QA}\cdot\frac{AR}{RB}=1$$





