歳差運動とは - 理数の散策路

歳差運動
コマの運動

歳差運動

歳差運動（さいさうんどう）とは、自転している物体の回転軸が、円を描くように動く現象です。

物体に固定されている座標を $\xi,\eta,\zeta$ とすると、外力がない場合のオイラーの運動方程式は以下になります。ここで $I_\xi,I_\eta,I_\zeta$ は主慣性モーメント、$\omega_\xi,\omega_\eta,\omega_\zeta$ は角速度を表します。

$$N_\xi=I_\xi\frac{d\omega_\xi}{dt}-(I_\eta-I_\zeta)\omega_\eta\omega_\zeta$$$$N_\eta=I_\eta\frac{d\omega_\eta}{dt}-(I_\zeta-I_\xi)\omega_\zeta\omega_\xi$$$$N_\zeta=I_\zeta\frac{d\omega_\zeta}{dt}-(I_\xi-I_\eta)\omega_\xi\omega_\eta$$

地球やコマのような対称形の物体は、３つの主慣性モーメントの内の２つが等しくなるため、

$$I_\xi=I_\eta\equiv I_1　,　I_\zeta\equiv I_3　　-①$$

と置くと、この物体の回転は以下の特徴を持ちます。この２つ目の特徴が歳差運動を表します。（②の導出）（③の導出）

$\zeta$ 軸方向の角速度 $\omega_\zeta$ は一定となります。$$\omega_\zeta=\Omega　　-②$$
角速度ベクトル ${\bf \omega}$ の大きさは一定で、その方向は $\zeta$ 軸と一定の角度を保ちつつ、その周りを角速度 $\lambda$ で回転します。ここで $a$ は定数です。$$(\omega_\xi,\omega_\eta)=(a\cos{\lambda t},-a\sin{\lambda t})　　-③$$$$\lambda=\frac{I_1-I_3}{I_1}\Omega$$

②の導出

オイラーの運動方程式に①の条件を適用すると、

$$I_1\frac{d\omega_\xi}{dt}=(I_1-I_3)\omega_\eta\omega_\zeta　　-(1)$$$$I_1\frac{d\omega_\eta}{dt}=(I_3-I_1)\omega_\zeta\omega_\xi　　-(2)$$$$\frac{d\omega_\zeta}{dt}=0　　-(3)$$

(3)より、$\zeta$ 軸方向の角速度 $\omega_\zeta$ は一定（特徴１）が導かれます。

③の導出

(1)と(2)を $\Omega$ と $\lambda$ を使って表すと、

$$\frac{d\omega_\xi}{dt}=\lambda\omega_\eta$$$$\frac{d\omega_\eta}{dt}=-\lambda\omega_\xi$$

これらの連立微分方程式は、$\tilde{\omega}=\omega_\xi+i\omega_\eta$ と置くと以下のように表されます。

$$\frac{d\tilde{\omega}}{dt}=-i\lambda\tilde{\omega}$$

これを積分すると、定数 $a$ より、

$$\tilde{\omega}=ae^{-i\lambda t}$$

これを実数部と虚数部を分けて書くと、

$$(\omega_\xi,\omega_\eta)=(a\cos{\lambda t},-a\sin{\lambda t})$$

これより $\omega_\xi$ と $\omega_\eta$ は、半径が一定（$=a$）の円を描く（特徴２）ことが分かります。

コマの運動

以下は重力の作用を受けている対称コマの運動を考えます。ここで、対称軸上の一点が固定されており、その点を原点 $O$ とします。空間に固定した座標を（$x,y,z$）、コマに固定した座標をとし（$\xi,\eta,\zeta$）、そして $O\zeta$ をコマの軸と定めます。

座標（$x,y,z$）と座標（$\xi,\eta,\zeta$）の関係を以下のオイラー角を使って表します。オイラー角では、初期の状態として座標（$x,y,z$）と座標（$\xi,\eta,\zeta$）を一致させ、次の３つの回転操作により、一般的な（$\xi,\eta,\zeta$）の方向を定めます。

回転１：$z$ 軸の周りを $\phi$ 回転させる。
回転２：$\eta$ 軸（$\eta’$ 軸）の周りを $\theta$ 回転させる。
回転３：$\zeta$ 軸の周りを $\psi$ 回転させる。

オイラー角とは

三次元空間の２つの直交座標系の関係を表す方法、回転行列、単位ベクトルの変換、任意のベクトル変換

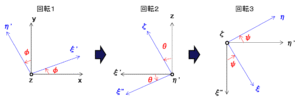
これら３つの座標変換は、行列を使って表現できます。ここで、各回転（$\phi,\theta,\psi$）の回転軸方向の単位ベクトルを（${\bf e}_\phi,{\bf e}_\theta,{\bf e}_\psi$）、座標（$\xi,\eta,\zeta$）の各軸方向の単位ベクトルを（${\bf e}_\xi,{\bf e}_\eta,{\bf e}_\zeta$）と定めると、単位ベクトルの変換は以下の回転行列で表すことができます。

$$\left(\begin{array}{ccc} {\bf e}_{\xi^{”}} \\ {\bf e}_\theta \\ {\bf e}_{\zeta} \end{array}\right)=
\left(\begin{array}{ccc} \cos{\theta} & 0 & -\sin{\theta} \\
0 & 1 & 0 \\
\sin{\theta} & 0 & \cos{\theta} \end{array}\right)
\left(\begin{array}{ccc} {\bf e}_{\xi’} \\ {\bf e}_\theta \\ {\bf e}_\phi \end{array}\right)　　-⑤$$$$\left(\begin{array}{ccc} {\bf e}_{\xi} \\ {\bf e}_{\eta} \\ {\bf e}_{\zeta} \end{array}\right)=
\left(\begin{array}{ccc} \cos{\psi} & \sin{\psi} & 0 \\
-\sin{\psi} & \cos{\psi} & 0 \\
0 & 0 & 1 \end{array}\right)
\left(\begin{array}{ccc} {\bf e}_{\xi^{”}} \\ {\bf e}_\theta \\ {\bf e}_{\zeta} \end{array}\right)　　-⑥$$

尚、回転１の回転軸は $z$ 軸であるため ${\bf e}_\phi={\bf e}_z$ 、回転２（⑤）の回転軸は $\eta’$ 軸であるため ${\bf e}_\theta={\bf e}_{\eta’}$ 、回転３（⑥）の回転軸は $\zeta$ 軸であるため ${\bf e}_\psi={\bf e}_\zeta$ となります。

コマの運動方程式

コマの角速度 ${\bf\omega}$ は、（$\dot{\phi},\dot{\theta},\dot{\psi}$）は各回転軸回りの角速度を表すため、

$${\bf\omega}=\dot{\phi}{\bf e}_\phi+\dot{\theta}{\bf e}_\theta+\dot{\psi}{\bf e}_\psi　　-⑦$$

これを座標 $O-\xi\eta\zeta$ に変換すると以下が得られます。（⑧の導出）

$$\omega_\xi=-\dot{\phi}\sin{\theta}\cos{\psi}+\dot{\theta}\sin{\psi}　　-⑧$$$$\omega_\eta=\dot{\phi}\sin{\theta}\sin{\psi}+\dot{\theta}\cos{\psi}　　-⑧$$$$\omega_\zeta=\dot{\phi}\cos{\theta}+\dot{\psi}　　-⑧$$

力のモーメント ${\bf N}$ は、固定点 $O$ から重心までの距離を $L$ 、質量を $M$ とすると、${\bf e}_\theta$ と方向が一致するため、

$${\bf N}=MgL\sin{\theta}{\bf e}_\theta　　-⑨$$

これを座標 $O-\xi\eta\zeta$ に変換すると以下が得られます。（⑩の導出）

$$N_\xi=MgL\sin{\theta}\sin{\psi}　　-⑩$$$$N_\eta=MgL\sin{\theta}\cos{\psi}　　-⑩$$$$N_\zeta=0　　-⑩$$

以上より、オイラーの方程式は以下になります。

$$I_1\frac{d}{dt}(\dot{\theta}\sin{\psi}-\dot{\phi}\sin{\theta}\cos{\psi})=MgL\sin{\theta}\sin{\psi}$$$$+(I_1-I_3)(\dot{\theta}\cos{\psi}+\dot{\phi}\sin{\theta}\sin{\psi})(\dot{\phi}\cos{\theta}+\dot{\psi})　　-⑪$$$$I_1\frac{d}{dt}(\dot{\theta}\cos{\psi}+\dot{\phi}\sin{\theta}\sin{\psi})=MgL\sin{\theta}\cos{\psi}$$$$+(I_3-I_1)(\dot{\theta}\sin{\psi}-\dot{\phi}\sin{\theta}\cos{\psi})(\dot{\phi}\cos{\theta}+\dot{\psi})　　-⑫$$$$I_3\frac{d}{dt}(\dot{\phi}\cos{\theta}+\dot{\psi})=0　　-⑬$$

⑧⑩の導出

⑤と⑥より ${\bf e}_\phi$ と ${\bf e}_\theta$ を（${\bf e}_\xi,{\bf e}_\eta,{\bf e}_\zeta$）で表すと、

$${\bf e}_\phi=-\sin{\theta}\cos{\psi}{\bf e}_\xi+\sin{\theta}\sin{\psi}{\bf e}_\eta+\cos{\theta}{\bf e}_\zeta　　-(1)$$$${\bf e}_\theta=\sin{\psi}{\bf e}_\xi+\cos{\psi}{\bf e}_\eta　　-(2)$$

(1)と(2)を⑦に代入すると⑧が得られ、(2)を⑨に代入すると⑩が得られます。

コマの運動の特徴

オイラーの方程式⑨を解くと、コマの運動には以下の保存則が成り立つことが分かります。

角速度の保存
⑬より $\zeta$ 軸方向の角速度 $\omega_\zeta$ は一定となります。$$\omega_\zeta=\dot{\phi}\cos{\theta}+\dot{\psi}=\Omega=\mathrm{const}　　-⑭$$
角運動量の保存
$z$ 軸方向の角運動量 $L_z$ は一定となります。（⑮の導出）$$L_z=I_1\dot{\phi}\sin^2{\theta}+I_3\Omega\cos{\theta}=\mathrm{const}　　-⑮$$
運動エネルギーの保存
ここで $\omega_A$ は $\xi^{”}$ 軸周りの角速度を表します。（⑯の導出）
$$\frac{1}{2}I_1(\omega_A^2+\omega_\theta^2)+MgL\cos{\theta}=\mathrm{const}　　-⑯$$

⑮の導出

⑪に $\cos{\psi}$ を掛け、⑫に $-\sin{\psi}$ を掛けて加えると、

$$\ddot{\phi}\sin{\theta}+\dot{\phi}\dot{\theta}\cos{\theta}-\dot{\theta}\dot{\psi}+\frac{I_1-I_3}{I_1}\Omega\dot{\theta}\sin{\theta}=0$$$$\frac{d}{dt}(\dot{\phi}\sin^2{\theta})-\dot{\theta}\sin{\theta}(\dot{\phi}\cos{\theta}+\dot{\psi})+\frac{I_1-I_3}{I_1}\Omega\dot{\theta}\sin{\theta}=0$$$$\frac{d}{dt}(\dot{\phi}\sin^2{\theta})-\frac{I_3}{I_1}\Omega\dot{\theta}\sin{\theta}=0$$

これを積分すると⑮の右辺が得られます。

$$I_1\dot{\phi}\sin^2{\theta}+I_3\Omega\cos{\theta}=\mathrm{const}　　\to⑮$$

これが $L_z$ に等しいことは以下のように確認できます。⑤と⑥より、

$${\bf e}_\xi=\cos{\psi}\cos{\theta}{\bf e}_{\xi’}+\sin{\psi}{\bf e}_\theta-\cos{\psi}\sin{\theta}{\bf e}_\phi$$$${\bf e}_\eta=-\sin{\psi}\cos{\theta}{\bf e}_{\xi’}+\cos{\psi}{\bf e}_\theta+\sin{\psi}\sin{\theta}{\bf e}_\phi$$$${\bf e}_\zeta=\sin{\theta}{\bf e}_{\xi’}+\cos{\theta}{\bf e}_\phi$$

角運動量にこれらを代入し、

$${\bf L}=I_1\omega_\xi{\bf e}_\xi+I_1\omega_\eta{\bf e}_\eta+I_3\omega_\zeta{\bf e}_\zeta$$

${\bf e}_z={\bf e}_\phi$ に注意して $L_z$ を求め、⑧を代入すると、

$$L_z={\bf L}\cdot{\bf e}_z=-I_1\omega_\xi\cos{\psi}\sin{\theta}+I_1\omega_\eta\sin{\psi}\sin{\theta}+I_3\omega_\zeta\cos{\theta}$$$$=I_1\dot{\phi}\sin^2{\theta}+I_3\omega_\zeta\cos{\theta}$$

$\omega_\zeta=\Omega$ であるから、これが⑮の右辺に等しいことが分かります。

⑯の導出

⑪に $\sin{\psi}$ を掛け、⑫に $\cos{\psi}$ を掛けて加えると、

$$I_1\ddot{\theta}+I_1\dot{\phi}\dot{\psi}\sin{\theta}-(I_1-I_3)\Omega\dot{\phi}\sin{\theta}=MgL\sin{\theta}　　-⑰$$

⑭と⑮を用いて $\dot{\phi}$ と $\dot{\psi}$ を消去すると、

$$\ddot{\theta}-\Big(\frac{L_z-I_3\Omega\cos{\theta}}{I_1\sin^2{\theta}}\Big)^2\cos{\theta}\sin{\theta}+\frac{I_3\Omega}{I_1}\Big(\frac{L_z-I_3\Omega\cos{\theta}}{I_1\sin{\theta}}\Big)=\frac{MgL}{I_1}\sin{\theta}$$$$\frac{1}{2}\frac{d}{dt}\Big[\dot{\theta}^2+\Big(\frac{L_z-I_3\Omega\cos{\theta}}{I_1\sin{\theta}}\Big)^2\Big]=-\frac{d}{dt}\Big(\frac{MgL}{I_1}\cos{\theta}\Big)$$

これを積分し、$L_z$ に再び⑮を代入すると、

$$\frac{I_1}{2}\Big[\dot{\theta}^2+\Big(\frac{L_z-I_3\Omega\cos{\theta}}{I_1\sin{\theta}}\Big)^2\Big]+MgL\cos{\theta}=\mathrm{const}$$$$\frac{I_1}{2}(\dot{\theta}^2+\dot{\phi}^2\sin^2{\theta})+MgL\cos{\theta}=\mathrm{const}　　-(3)$$

ここで⑤より、${\bf e}_\phi$ を ${\bf e}_{\xi^{”}},{\bf e}_\zeta$ で表すと、

$${\bf e}_\phi=-\sin{\theta}{\bf e}_{\xi^{”}}+\cos{\theta}{\bf e}_\zeta$$

これを⑦を代入すると、${\bf e}_\psi={\bf e}_\zeta$ であるから、

$${\bf\omega}=-\dot{\phi}\sin{\theta}{\bf e}_{\xi^{”}}+\dot{\theta}{\bf e}_\theta+(\dot{\psi}+\dot{\phi}\cos{\theta}){\bf e}_\zeta$$

従って $\omega_{\xi^{”}}=-\dot{\phi}\sin{\theta}$ 、$\omega_\theta=\dot{\theta}$ であるから、これを(3)に代入すると、

$$\frac{I_1}{2}(\omega_{\xi^{”}}^2+\omega_\theta^2)+MgL\cos{\theta}=\mathrm{const}$$

尚、⑯では $\omega_{\xi^{”}}=\omega_A$ と置き換えています。

定常歳差運動

コマの運動における歳差運動とは、$\phi$ の変化を指します。$\theta$ を一定とし、⑰で $\dot{\theta}=0$ とすると、

$$I_1\dot{\phi}^2\cos{\theta}-I_3\Omega\dot{\phi}+MgL=0$$

これを $\dot{\phi}$ について解くと、

$$\dot{\phi}=\frac{I_3\Omega}{2I_1\cos{\theta}}\left(1\pm\sqrt{1-\frac{4MgLI_1\cos{\theta}}{I_3^2\Omega^2}}\right)$$

この根号内は負にはならないので、その条件は、

$$\Omega\ge\frac{\sqrt{4MgLI_1\cos{\theta}}}{I_3}　　-(4)$$

速い歳差運動
(4)で等号が成り立つ場合は以下になります。
$$\dot{\phi}=\frac{I_3\Omega}{2I_1\cos{\theta}}$$
遅い歳差運動
$\Omega$ が十分に大きい（根号内の第２項が十分に小さい）とすると、
$$\dot{\phi}=\frac{MgL}{I_3\Omega}$$

実際のコマでは、速い歳差運動は摩擦によってすぐに減衰し、遅い歳差運動だけが観察されます。また、$g=0$ の自由回転では速い歳差運動だけが存在します。