オイラー角
オイラー角とは、三次元空間の2つの直交座標系の関係を表す方法の1つです。 レオンハルト・オイラーにより考案されました。
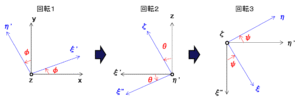
2つの直交座標系を($x,y,z$)と($\xi,\eta,\zeta$)とします。初期の状態として座標($x,y,z$)と座標($\xi,\eta,\zeta$)を一致させ、次の3つの回転操作により、一般的な($\xi,\eta,\zeta$)の方向を定めます。
- 回転1:$z$ 軸の周りを $\phi$ 回転させる。
- 回転2:$\eta$ 軸($\eta’$ 軸)の周りを $\theta$ 回転させる。
- 回転3:$\zeta$ 軸の周りを $\psi$ 回転させる。
| 初期 | 回転1($\phi$) | 回転2($\eta$) | 回転3($\zeta$) |
| $x$ | $\to\xi’$ | $\to\xi^{”}$ | $\to\xi$ |
| $y$ | $\to\eta’$ | 回転軸:$\eta’$ | $\to\eta$ |
| $z$ | 回転軸:$z$ | $\to\zeta$ | 回転軸:$\zeta$ |
回転行列
これら3つの座標変換は、行列を使って表現できます。
$$\left(\begin{array}{ccc} \xi’ \\ \eta’ \\ z \end{array}\right)=
\left(\begin{array}{ccc} \cos{\phi} & \sin{\phi} & 0 \\
-\sin{\phi} & \cos{\phi} & 0 \\
0 & 0 & 1 \end{array}\right)
\left(\begin{array}{ccc} x \\ y \\ z \end{array}\right) -①$$$$\left(\begin{array}{ccc} \xi^{”} \\ \eta’ \\ \zeta \end{array}\right)=
\left(\begin{array}{ccc} \cos{\theta} & 0 & -\sin{\theta} \\
0 & 1 & 0 \\
\sin{\theta} & 0 & \cos{\theta} \end{array}\right)
\left(\begin{array}{ccc} \xi’ \\ \eta’ \\ z \end{array}\right) -②$$$$\left(\begin{array}{ccc} \xi \\ \eta \\ \zeta \end{array}\right)=
\left(\begin{array}{ccc} \cos{\psi} & \sin{\psi} & 0 \\
-\sin{\psi} & \cos{\psi} & 0 \\
0 & 0 & 1 \end{array}\right)
\left(\begin{array}{ccc} \xi^{”} \\ \eta’ \\ \zeta \end{array}\right) -③$$
ここで、各回転($\phi,\theta,\psi$)の回転軸方向の単位ベクトルを(${\bf e}_\phi,{\bf e}_\theta,{\bf e}_\psi$)、座標($x,y,z$)の各軸方向の単位ベクトルを(${\bf e}_x,{\bf e}_y,{\bf e}_z$)、座標($\xi,\eta,\zeta$)の各軸方向の単位ベクトルを(${\bf e}_\xi,{\bf e}_\eta,{\bf e}_\zeta$)と定めます。②と③を単位ベクトル書き直すと。
$$\left(\begin{array}{ccc} {\bf e}_{\xi’} \\ {\bf e}_{\eta’}(={\bf e}_\theta) \\ {\bf e}_z(={\bf e}_\phi) \end{array}\right)=
\left(\begin{array}{ccc} \cos{\phi} & \sin{\phi} & 0 \\
-\sin{\phi} & \cos{\phi} & 0 \\
0 & 0 & 1 \end{array}\right)
\left(\begin{array}{ccc} {\bf e}_x \\ {\bf e}_y \\ {\bf e}_z(={\bf e}_\phi) \end{array}\right) -④$$$$\left(\begin{array}{ccc} {\bf e}_{\xi^{”}} \\ {\bf e}_{\eta’}(={\bf e}_\theta) \\ {\bf e}_{\zeta}(={\bf e}_\psi) \end{array}\right)=
\left(\begin{array}{ccc} \cos{\theta} & 0 & -\sin{\theta} \\
0 & 1 & 0 \\
\sin{\theta} & 0 & \cos{\theta} \end{array}\right)
\left(\begin{array}{ccc} {\bf e}_{\xi’} \\ {\bf e}_{\eta’}(={\bf e}_\theta) \\ {\bf e}_z(={\bf e}_\phi) \end{array}\right) -⑤$$$$\left(\begin{array}{ccc} {\bf e}_{\xi} \\ {\bf e}_{\eta} \\ {\bf e}_{\zeta}(={\bf e}_\psi) \end{array}\right)=
\left(\begin{array}{ccc} \cos{\psi} & \sin{\psi} & 0 \\
-\sin{\psi} & \cos{\psi} & 0 \\
0 & 0 & 1 \end{array}\right)
\left(\begin{array}{ccc} {\bf e}_{\xi^{”}} \\ {\bf e}_{\eta’}(={\bf e}_\theta) \\ {\bf e}_{\zeta}(={\bf e}_\psi) \end{array}\right) -⑥$$
尚、④の回転軸は $z$ 軸であるため ${\bf e}_\phi={\bf e}_z$ 、⑤の回転軸は $\eta’$ 軸であるため ${\bf e}_\theta={\bf e}_{\eta’}$ 、⑥の回転軸は $\zeta$ 軸であるため ${\bf e}_\psi={\bf e}_\zeta$ となります。
ベクトルの変換
単位ベクトルの変換④~⑥より、任意のベクトル ${\bf A}$ は($x,y,z$)、($\xi,\eta,\zeta$)、($\phi,\theta,\psi$)の各座標間で変換することができます。以下は例を挙げます。
- ($x,y,z$)⇒($\xi,\eta,\zeta$)の変換は以下になります。
$${\bf A}=A_x{\bf e}_x+A_y{\bf e}_y+A_z{\bf e}_z=A_\xi{\bf e}_\xi+A_\eta{\bf e}_\eta+A_\zeta{\bf e}_\zeta$$$${\bf e}_x=(\cos{\phi}\cos{\theta}\cos{\psi}-\sin{\phi}\sin{\psi}){\bf e}_\xi$$$$-(\cos{\phi}\cos{\theta}\sin{\psi}+\sin{\phi}\cos{\psi}){\bf e}_\eta+\cos{\phi}\sin{\theta}{\bf e}_\zeta$$$${\bf e}_y=(\sin{\phi}\cos{\theta}\cos{\psi}+\cos{\phi}\sin{\psi}){\bf e}_\xi$$$$-(\sin{\phi}\cos{\theta}\sin{\psi}-\cos{\phi}\cos{\psi}){\bf e}_\eta+\sin{\phi}\sin{\theta}{\bf e}_\zeta$$$${\bf e}_z=-\sin{\theta}\cos{\psi}{\bf e}_\xi+\sin{\theta}\sin{\psi}{\bf e}_\eta+\cos{\theta}{\bf e}_\zeta$$
- ($\phi,\theta,\psi$)⇒($\xi,\eta,\zeta$)の変換は以下になります。
$${\bf A}=A_\phi{\bf e}_\phi+A_\theta{\bf e}_\theta+A_\psi{\bf e}_\psi=A_\xi{\bf e}_\xi+A_\eta{\bf e}_\eta+A_\zeta{\bf e}_\zeta$$$${\bf e}_\phi=-\sin{\theta}\cos{\psi}{\bf e}_\xi+\sin{\theta}\sin{\psi}{\bf e}_\eta+\cos{\theta}{\bf e}_\zeta$$$${\bf e}_\theta=\sin{\psi}{\bf e}_\xi+\cos{\psi}{\bf e}_\eta$$$${\bf e}_\psi={\bf e}_\zeta$$




