弦の運動量
ラグラジアンの対称性による保存量(カレント)の概念を、弦の世界面に対して適用します。「ラグラジアン密度の対称性」で用いた作用の定義
$$S=\int{\mathcal L}\Big(\phi^\mu(q),\partial_a\phi^\mu(q)\Big)dq^0\cdots dq^d$$$$\partial_a\phi^\mu\equiv\frac{\partial\phi^\mu}{\partial q^a}$$
に対して、以下のように、場の変数 $\phi^\mu$ を弦の座標 $X^\mu$ に、座標 $q^a$ を弦の世界面(2次元)に対応を行うと、
$$\phi^\mu \to X^\mu$$$$(q^0,\cdots,q^d) \to (\tau,\sigma)$$
以下の南部・後藤の作用が得られます。
$$S=\int{\mathcal L}(\partial_\tau X^\mu,\partial_\sigma X^\mu)d\tau d\sigma$$
弦の世界面上のカレント
「ラグラジアン密度の対称性」で定義したカレントを弦の世界面に適用すると、定義より、(①②を導く)
$$J_\mu^\tau=\frac{\partial{\mathcal L}}{\partial(\partial_\tau X^\mu)}=P_\mu^\tau -①$$$$J_\mu^\sigma=\frac{\partial{\mathcal L}}{\partial(\partial_\sigma X^\mu)}=P_\mu^\sigma -②$$
このカレントの保存則は以下で表されます。これは、相対論的弦の運動方程式であることが分かります。
$$\partial_a J_\mu^a=\frac{\partial P_\mu^\tau}{\partial\tau}+\frac{\partial P_\mu^\sigma}{\partial\sigma}=0 -③$$
弦の世界面上のチャージ
「ラグラジアン密度の対称性」で定義したチャージは、カレントの第0成分を空間積分することで得られますが、
$$Q_\mu=\int J_\mu^0dq^1\cdots dq^d$$
弦の世界面に適用すると、チャージは弦の運動量 $p_\mu$ に相当します。
$$p_\mu(\tau)=\int_0^{\sigma1}P_\mu^\tau(\tau,\sigma)d\sigma -④$$
この弦の運動量は、次のように一般化することができ、(⑤を導く)
$$p_\mu=\int_c(P_\mu^\tau d\sigma-P_\mu^\sigma d\tau) -⑤$$
以下のような保存則が成り立ちます。ここでは静的ゲージ $\tau=t$ を選択しています。(⑥を導く)
$$\frac{dp_\mu}{d\tau}=\frac{dp_\mu}{dt}=0 -⑥$$
導出
①と②の導出
カレントの定義式は以下であるため、
$$\epsilon^\mu J_\mu^a\equiv\frac{\partial{\mathcal L}}{\partial(\partial_a\phi)}\delta\phi$$
ここで $\tau$ 成分について考え、 $\phi\to X^\mu$、$\delta\phi=\delta X^\mu=\epsilon^\mu$($\epsilon^\mu$ は定数)と置き替えると、
$$\epsilon^\mu J_\mu^\tau=\frac{\partial{\mathcal L}}{\partial\dot{X}^\mu}\epsilon^\mu$$
さらに、$\dot{X}^\mu$ の共役変数 $P_\mu^\tau$ は以下で定義されるため、
$$P^\tau_\mu\equiv\frac{\partial{\mathcal L}}{\partial\dot{X}^\mu}$$
これらより①が導かれます。また、$\sigma$ 成分も同様にして、②を導くことができます。
⑤の導出
④と⑤が等しいことを示します。まず、2次元の発散定理は以下であるため、
$$\oint(A^xdy-A^ydx)=\int_S\Big(\frac{\partial A^x}{\partial x}+\frac{\partial A^y}{\partial y}\Big)dxdy$$
これを以下のように書き換えることができます。最後が0になるは、被積分が0(相対論的弦の運動方程式)であるためです。
$$\oint(P_\mu^\tau d\sigma-P_\mu^\sigma d\tau)=\int\Big(\frac{\partial P_\mu^\tau}{\partial\tau}+\frac{\partial P_\mu^\sigma}{\partial\sigma}\Big)d\tau d\sigma=0 -(1)$$
左辺の積分を、下図のような世界面上($\tau,\sigma$)の閉領域の積分($a\to b\to c\to d$)と考えます。ここで、経路 $c$ は端点($\sigma=0,\sigma=\sigma_1$)を結ぶ任意の経路です。
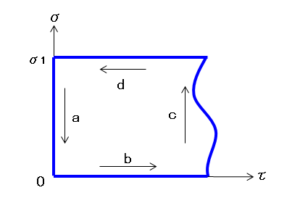
このとき、(1)は以下のように書き換えられます。
$$0=\oint(P_\mu^\tau d\sigma-P_\mu^\sigma d\tau)$$$$=\Big(-\int_a+\int_b+\int_c-\int_d\Big)(P_\mu^\tau d\sigma-P_\mu^\sigma d\tau)$$
経路 $b,d$ 上では $d\sigma=0$、さらに自由端点の境界条件
$$P_\mu^\sigma(\tau,0)=P_\mu^\sigma(\tau,\sigma_1)=0 -⑦$$
を使うと、経路 $b,d$ 上の積分は0になります。また、$a$ 上では $d\tau=0$であるため、(1)は以下のように簡略化されます。
$$0=-\int_aP_\mu^\tau d\sigma+\int_c(P_\mu^\tau d\sigma-P_\mu^\sigma d\tau)$$
この結果より⑤が得られることが分かります。
$$\int_0^{\sigma_1}P_\mu^\tau d\sigma=\int_c(P_\mu^\tau d\sigma-P_\mu^\sigma d\tau)$$
⑥を導く
⑥の左辺に④と③を代入すると、
$$\frac{dp_\mu}{d\tau}=\int_0^{\sigma1}\frac{dP_\mu^\tau}{d\tau}d\sigma$$$$=-\int_0^{\sigma1}\frac{dP_\mu^\sigma}{d\sigma}d\sigma=\Big[P_\mu^\sigma\Big]_0^{\sigma_1}$$
自由端点の境界条件⑦を使うと以下になり、$p_\mu$ が保存されることが得られます。
$$\frac{dp_\mu}{d\tau}=0$$




