初等関数
指数関数
指数関数とは、以下のように冪における指数 $x$ を変数とする関数ですが、
$$y=a^x$$
狭義では、以下のネイピア数 $e$ を底とする指数関数を指します。
$$y=e^x$$$$e\equiv\lim_{n \to \infty}\Big(1+\frac{1}{n}\Big)^n\cong2.718$$
指数法則
$p,q$ を有理数、$a,b\gt0$ とすると以下の関係が成り立ちます。
- $a^pa^q=a^{p+q}$ 、$a^p/a^q=a^{p-q}$
- $(a^p)^q=^{pq}$ 、$(ab)^p=a^pb^p$
累乗根
$m,n$ を正の整数、$a,b\gt0$ とすると以下の関係が成り立ちます。
- $a^{m/n}={}^n\sqrt{a^m}$ 、$a^{-m/n}=1/({}^n\sqrt{a^m})$
- $({}^n\sqrt{a})^n=a$ 、${}^n\sqrt{a}{}^n\sqrt{b}={}^n\sqrt{ab}$
- ${}^m\sqrt{{}^n\sqrt{a}}={}^{mn}\sqrt{a}$ 、${}^n\sqrt{a^m}={}^{nl}\sqrt{a^{ml}}$
対数関数
対数関数 $\log$ の公式を指数との対比で整理します。
| 指数 | 対数 |
| $a^x=y$ | $x=\log_a{y}$ |
| $a^0=1$ | $0=\log_a{1}$ |
| $a^1=a$ | $1=\log_a{a}$ |
| $a^x\cdot a^y = a^{x+y}$ | $\log_a{xy}=\log_a{x}+\log_a{y} -①$ |
| $$\frac{a^x}{a^y}=a^{x-y}$$ | $$\log_a{\frac{x}{y}}=\log_a{x}-\log_a{y} -②$$ |
| $a^y=x^b$（$a^{y/b}=x$） | $\log_a{x^b}=b\log_a{x} -③$ |
| $x=a^y$ | $$\log_a{x}=\frac{\log_b{x}}{\log_b{a}} -④$$ |
導出
［③の導出］
$a^y=x^b$ の対数を取ると $y=\log_a{x^b}$ 、$a^{y/b}=x$ の対数を取ると $y/b=\log_a{x}$ より、$y$ を削除すると対数の公式が得られます。
［④の導出］
$x=a^y$ を $a$ と $b$ で対数を取ると $\log_a{x}=y$ 、$\log_b{x}=y\log_b{a}$ より、$y$ を削除すると対数の公式が得られます。
三角関数
三角関数は直角三角形の各辺の比として定義されます。
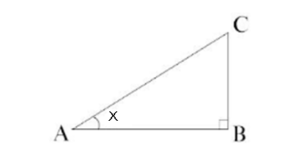
$$\sin{x}\equiv\frac{BC}{AC}$$$$\cos{x}\equiv\frac{AB}{AC}$$$$\tan{x}\equiv\frac{BC}{AB}=\frac{\sin{x}}{\cos{x}}$$$$\sec{x}=\frac{1}{\cos{x}}$$$$\mathrm{cosec}\,x=\csc{x}=\frac{1}{\sin{x}}$$$$\cot{x}=\frac{1}{\tan{x}}$$
三角関数の性質
三角関数の０、$\pi/2$ 、$\pi$ 、$3\pi/2$ 前後の書き換えは以下になります。
| ０ | $\sin{(\pm\theta)} =\pm\sin{\theta}$ $\cos{(\pm\theta)} =\cos{\theta}$ $\tan{(\pm\theta)} =\pm\tan{\theta}$ |
| $\pi/2$ | $\sin{(\pi/2\pm\theta)} =\cos{\theta}$ $\cos{(\pi/2\pm\theta)} =\mp\sin{\theta}$ $\tan{(\pi/2\pm\theta)} =\mp1/\tan{\theta}$ |
| $\pi$ | $\sin{(\pi\pm\theta)} =\mp\sin{\theta}$ $\cos{(\pi\pm\theta)} =-\cos{\theta}$ $\tan{(\pi\pm\theta)} =\pm\tan{\theta}$ |
| $3\pi/2$ | $\sin{(3\pi/2\pm\theta)} =-\cos{\theta}$ $\cos{(3\pi/2\pm\theta)} =\pm\sin{\theta}$ |
| $2\pi$ | $\sin{(2\pi\pm\theta)} =\sin{\theta}$ $\cos{(2\pi\pm\theta)} =\sin{\theta}$ |
弧度法
三角関数では弧度法が使われます。弧度法では、180°を $\pi$ ラジアンで定義します。半径 $r$ 、中心角 $\theta$ の扇形の弧の長さ $l$ と面積は $S$ 以下で表されます。
$$l=r\theta$$$$S=\frac{1}{2}r^2\theta=\frac{1}{2}lr$$
三角関数の関係式
三角関数には以下の関係式が成り立ちます。
$$\sin^2{x}+\cos^2{x}=1$$$$\sin{x}\lt x\lt\tan{x} (0\le x\le \pi/2)$$$$\lim_{x\to0}\frac{\sin x}{x}=1$$$$\tan{x}=\frac{\sin{x}}{\cos{x}}$$$$1+\tan^2{x}=\frac{1}{\cos^2{x}}$$
加法定理
三角関数の加法定理は以下になります。以下の式は⑥と⑦より導くことができます。
$$\sin{(x\pm y)}=\sin{x}\cos{y}\pm\cos{x}\sin{y}$$$$\cos{(x\pm y)}=\cos{x}\cos{y}\mp\sin{x}\sin{y}$$$$\tan{(x\pm y)}=\frac{\tan{x}\mp\tan{y}}{1\mp\tan{x}\tan{y}}$$$$\sin{x}\pm\sin{y}=2\sin{\frac{x\pm y}{2}}\cos{\frac{x\mp y}{2}}$$$$\cos{x}+\cos{y}=2\cos{\frac{x+y}{2}}\cos{\frac{x-y}{2}}$$$$\cos{x}-\cos{y}=-2\sin{\frac{x+y}{2}}\sin{\frac{x-y}{2}}$$
２倍角と半角の公式
加法定理より２倍角の公式は以下で、
$$\sin{2x}=2\sin{x}\cos{x}$$$$\cos{2x}=\cos^2{x}-\sin^2{x}$$$$\tan{2x}=\frac{2\tan{x}}{1-\tan^2{x}}$$
半角の公式は以下で表されます。
$$\sin^2{\frac{x}{2}}=\frac{1-\cos{x}}{2}$$$$\cos^2{\frac{x}{2}}=\frac{1+\cos{x}}{2}$$$$\tan^2{\frac{x}{2}}=\frac{1-\cos{x}}{1+\cos{x}}$$
三角関数の合成
三角形の合成は以下で表されます。
$$a\sin{\theta}+b\cos{\theta}=\sqrt{a^2+b^2}\sin{(\theta+\alpha)}$$$$\sin{\alpha}=\frac{b}{\sqrt{a^2+b^2}}$$$$\cos{\alpha}=\frac{a}{\sqrt{a^2+b^2}}$$
双曲線関数
双曲線関数は以下で定義されます。
$$\cosh{x}\equiv\frac{e^x+e^{-x}}{2} -⑧$$$$\sinh{x}\equiv\frac{e^x-e^{-x}}{2} -⑨$$$$\tanh{x}\equiv\frac{\sinh{x}}{\cosh{x}}$$
双曲線関数の関係式
双曲線関数には以下の関係式が成り立ちます。以下の式は⑧と⑨より導くことができます。
$$e^x=\cosh{x}+\sinh{x}$$$$\cosh^2{x}-\sinh^2{x}=1$$$$\sinh{x}=-i\sin{(ix)}$$$$\cosh{x}=\cos{(ix)}$$
加法定理
双曲線関数の加法定理は以下になります。以下の式は⑧と⑨より導くことができます。
$$\sinh{(x+y)}=\sinh{x}\cosh{y}+\cosh{x}\sinh{y}$$$$\cosh{(x+y)}=\cosh{x}\cosh{y}+\sinh{x}\sinh{y}$$$$\sinh{x}+\sinh{y}=2\sinh{\Big(\frac{x+y}{2}\Big)}\cosh{\Big(\frac{x-y}{2}\Big)}$$$$\cosh{x}+\cosh{y}=2\cosh{\Big(\frac{x+y}{2}\Big)}\cosh{\Big(\frac{x-y}{2}\Big)}$$
オイラーの公式
オイラーの公式により、指数関数と三角関数が関係が示されます。
$$e^{ix}=\cos{x}+i\sin{x} -⑤$$
オイラーの公式より、以下の関係式は導かれます。
$$e^{2\pi i}=1$$$$e^{ix}=e^{i(x+2n\pi)}$$$$\cos{x}=\frac{e^{ix}+e^{-ix}}{2} -⑥$$$$\sin{x}=\frac{e^{ix}-e^{-ix}}{2i} -⑦$$
⑤の導出
関数 $f(x)=e^{-ix}(\cos x +i\sin x)$ を定義します。両辺の微分をとると $f'(x)=0$ より、$f(x)$ は一定値となります。これより、$f(x)=f(0)=1$ と置き、両辺に $e^{ix}$ を掛けると⑤が得られます。
微分公式
微分とは、関数などの値の変化率を測るものです。関数 $f(x)$ の微分は次のように定義されます。
$$\frac{dy(x)}{dx}=\lim_{h \to0}\frac{y(x+h)-y(x)}{h}$$
べき関数
べき関数の微分は以下になります。
$$\frac{d}{dx}(x^a)=ax^{a-1}$$
これにより導関数の公式は以下になります。
- $c$ が定数で、$y=c$ ならば、$y’=0$
- $a,b$ が定数で、$y=af(x)\pm bg(x)$ ならば、$y’=af'(x)\pm bg'(x)$
導出
べき関数の微分は定義から求めることができます。$(x+h)^a$ をテイラー展開して、$h\to0$ としています。
$$\frac{d}{dx}(x^a)=\lim_{h\to0}\frac{(x+h)^a-x^a}{h}$$$$=
\lim_{h\to0}\frac{1}{h}\left[x^a\Big(1+\frac{ah}{x}+\frac{a(a-1)h^2}{x^2}+\cdots\Big)-x^a\right]=ax^{a-1}$$
指数関数
指数関数の微分は以下になります。
$$\frac{d}{dx}(a^x)=a^x \ln{a}$$$$\frac{d}{dx}(e^x)=e^x$$
導出
$a^h-1=1/t$（$h\to0$ で $t\to\infty$）と置くと、
$$h=\log_a\Big(1+\frac{1}{t}\Big)$$
微分の定義より、
$$\frac{d}{dx}(a^x)=a^x\lim_{h\to 0}\frac{a^h-1}{h}$$$$=
a^x\lim_{t\to\infty}\frac{1}{t\log_a\Big(1+\frac{1}{t}\Big)}=a^x\frac{1}{\log_ae}=a^x\ln{a}$$
途中、次のネイピア数の定義を使っています。
$$\lim_{t\to\infty}\Big(1+\frac{1}{t}\Big)^t=e$$
対数関数
対数関数の微分は以下になります。
$$\frac{d}{dx}\left(\log_ax\right)=\frac{1}{x\ln{a}}$$$$\frac{d}{dx}\left(\ln{x}\right)=\frac{1}{x}$$
導出
$\log_a{x}=y$ と置くと、$x=a^y$ であるから、両辺を $x$ で微分すると、
$$1=\frac{dy}{dx}a^y\ln{a}=\frac{dy}{dx}x\ln{a}$$
自然対数の場合は、$a=e$ と置くと得られます。
三角関数
三角関数の微分は以下になります。
$$\frac{d}{dx}(\sin{x})=\cos{x}$$$$\frac{d}{dx}(\cos{x})=-\sin{x}$$$$\frac{d}{dx}(\tan{x})=\frac{1}{\cos^2{x}}$$
導出
微分の定義式より、
$$\frac{d}{dx}(\sin{x})=\lim_{h\to0}\frac{\sin(x+h)-\sin x}{h}$$$$=
\lim_{h\to0}\frac{2\cos{\left(x+\frac{h}{2}\right)}\sin{\left(\frac{h}{2}\right)}}{h}=\cos{x}$$
$$\frac{d}{dx}(\cos{x})=\lim_{h\to0}\frac{\cos(x+h)-\cos x}{h}$$$$=
\lim_{h\to0}\frac{-2\sin{\left(x+\frac{h}{2}\right)}\sin{\left(\frac{h}{2}\right)}}{h}=-\sin{x}$$
ここで、次の近似を使っています。
$$\lim_{h\to0}\Big(\sin{\frac{h}{2}}\Big)=\frac{h}{2}$$
尚、$\tan$ については以下の計算より得られます。
$$\frac{d}{dx}(\tan{x})=\frac{d}{dx}\Big(\frac{\sin{x}}{\cos{x}}\Big)$$
双曲線関数
双曲線関数の微分は以下になります。
$$\frac{d}{dx}(\sinh{x})=\frac{d}{dx}\Big(\frac{e^x-e^{-x}}{2}\Big)=\cosh{x}$$
$$\frac{d}{dx}(\cosh{x})=\frac{d}{dx}\Big(\frac{e^x+e^{-x}}{2}\Big)=\sinh{x}$$
$$\frac{d}{dx}(\tanh{x})=\frac{d}{dx}\Big(\frac{\sinh{x}}{\cosh{x}}\Big)=\frac{1}{\cosh^2{x}}$$
$\tanh$ の計算では以下の関係式を使っています。
$$\cosh^2{x}-\sinh^2{x}=1$$
幾何学との関係
接線と法線
曲線 $y=f(x)$ 上の点 $A\big(a,f(a)\big)$ において、
- 接線の方程式
$$y-f(a)=f'(a)(x-a)$$ - 法線の方程式
$$y-f(a)=-\frac{1}{f'(a)}(x-a)$$
関数の形
- 関数の増減
関数 $f(x)$ が区間 $[a,b]$ で連続かつ微分可能ならば、
常に $f'(X)\gt0$ ならば区間 $[a,b]$ で単調増加
常に $f'(X)\lt0$ ならば区間 $[a,b]$ で単調減少
常に $f'(X)=0$ ならば区間 $[a,b]$ で定数 - 関数の極大・極小
$x=a$ を含む十分小さい区間について、
$x\ne a$ で $f(x)\lt f(a)$ のとき、$f(x)$ は $x=a$ で極大値をもつ
$x\ne a$ で $f(x)\gt f(a)$ のとき、$f(x)$ は $x=a$ で極小値をもつ - 極大値・極小値
$x=a$ を含むある区間で $f^{”}(x)$ は連続とすると、
$f'(a)=0$ 、$f^{”}(a)\lt 0$ ならば $f(a)$ は極大値
$f'(a)=0$ 、$f^{”}(a)\gt 0$ ならば $f(a)$ は極小値 - 凹凸と変曲点
ある区間で $f^{”}(a)\gt 0$ ならば、その区間で下に凸
ある区間で $f^{”}(a)\lt 0$ ならば、その区間で上に凸
曲線の凹凸が切り替わる曲線上の点 $f^{”}(a)=0$ を変曲点と呼ぶ - 漸近線
以下のどちらが $\pm\infty$ になる場合、直線 $x=a$ が漸近線
$$\lim_{x\to a+0}f(x) , \lim_{x\to a-0}f(x)$$
以下のどちらが $0$ になる場合、直線 $y=ax+b$ が漸近線
$$\lim_{x\to\infty}\Big(f(x)-(ax+b)\Big) , \lim_{x\to-\infty}\Big(f(x)-(ax+b)\Big)$$
物理学との関係
- 平面上の運動の速度 $v$
運動する点の座標 $x$ が時間 $t$ の関数 $x=f(t)$ 、$y=g(x)$ で表されるとき
$$\vec{v}=\Big(\frac{dx}{dt},\frac{dy}{dt}\Big)$$$$|\vec{v}|=\sqrt{\Big(\frac{dx}{dt}\Big)^2+\Big(\frac{dy}{dt}\Big)^2}$$ - 平面上の運動の加速度 $a$
$$\vec{a}=\Big(\frac{d^2x}{dt^2},\frac{d^2y}{dt^2}\Big)$$$$|\vec{a}|=\sqrt{\Big(\frac{d^2x}{dt^2}\Big)^2+\Big(\frac{d^2y}{dt^2}\Big)^2}$$
積分公式
不定積分の場合、$n$ が正の整数または０のとき、
$$\int x^ndx=\frac{1}{n+1}x^{n+1}+C$$
定積分の場合、$f(x)$ の原始関数の１つを $F(x)$ とすると、
$$\int_a^bf(x)dx=\Big[F(x)\Big]_a^b=F(b)-F(a)$$
初等関数の積分
$$\int\frac{dx}{x}=log_e|x|+C$$$$\int\sin{x}dx=-\cos{x}+C$$$$\int\cos{x}dx=\sin{x}+C$$$$\int e^xdx=e^x+C$$$$\int a^xdx=\frac{a^x}{\log_ea}+C$$
置換積分法と部分積分法
置換積分法は、
$$\int f\big(g(x)\big)g'(x)dx=\int f(u)du , g(x)\equiv u$$$$\int\frac{f'(x)}{f(x)}=\log_e{|f(x)|}+C$$
定積分の置換積分法は、$x=g(t)$ 、$a=g(p)$ 、$b=g(q)$ のとき、
$$\int_a^bf(x)dx=\int_p^qf\big(g(t)\big)g'(t)dt$$
部分積分法は、
$$\int f(x)g'(x)dx=f(x)g(x)-\int f'(x)g(x)dx$$$$\int f(x)dx=xf(x)-\int xf'(x)dx$$
定積分の部分積分法は、
$$\int_a^bf(x)g'(x)dx=\Big[f(x)g(x)\Big]_a^b-\int_a^bf'(x)g(x)dx$$
幾何学との関係
- 区間 $a\le x\le b$ において、$f(x)\ge g(x)$ であるとき、この２つの曲線に囲まれた面積は、
$$S=\int_a^b\Big(f(x)-g(x)\Big)dx$$ - 曲線 $x=g(y)$ と $y$ 軸の間の面積
曲線 $x=g(y)$ と $y$ 軸と２直線 $y=c$ 、$y=d$ で囲まれた面積
$$S=\int_c^d|g(y)|dy$$ - $x=f(t)$ 、$y=g(t)$ で表される面積
$$S=\int_a^bydx=\int_\alpha^\beta g(t)f'(x)dt$$$$a=f(\alpha) , b=f(\beta)$$ - 立体の体積
断面の面積が $S(x)$ の立体の $a\le x\le b$ での体積は、
$$V=\int_a^bS(x)dx$$ - 回転体の体積
曲線 $y=f(x)$ と $x$ 軸と２直線 $x=a$ 、$x=b$ で囲まれた部分を $x$ 軸の周りに１回転してできる立体の体積は、
$$V=\pi\int_a^b\Big(f(x)\Big)^2dx$$ - 曲線の長さ
曲線 $x=f(t)$ 、$y=g(t)$（ $\alpha\le t\le\beta$ ）の長さ $L$ は、
$$L=\int_\alpha^\beta\sqrt{\Big(\frac{dx}{dt}\Big)^2+\Big(\frac{dy}{dt}\Big)^2}dt$$
曲線 $y=f(x)$ （ $a\le x\le b$ ）の長さ $L$ は、
$$L=\int_a^b\sqrt{1+\Big(\frac{dy}{dx}\Big)^2}dx$$
