シンプソンの公式とは
シンプソンの公式とは、数値解析における数値積分の方法の1つです。シンプソンの公式では、定積分の積分領域を2つの組の小さな区間に分割し、その区間を2次関数で近似して積分を行います。
同様な数値積分法である台形公式では、分割した区間を1次関数(直線)で近似するため、シンプソンの公式は台形公式より精度の高い数値積分法であると言えます。
関数 $y=f(x)$ の積分領域 $[a,b]$ での定積分を考えます。積分領域を $2n$ 個の幅 $h$ の小さな区間を分け、隣り合う2つの区間の点の組を $(x_1,y_1)$ 、$(x_2,y_2)$ 、$(x_3,y_3)$ とします。
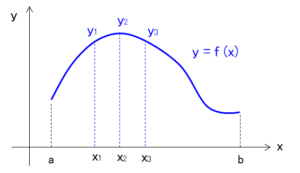
このとき、区間 $[x_1,x_3]$ の定積分は以下で近似されます。
$$\int_{x_1}^{x_3}f(x)dx=\frac{h}{3}(y_1+4y_2+y_3) -①$$$$h=x_2-x_1=x_3-x_2$$
これにより、区間 $[a,b]$ の定積分は以下で近似されます。
$$\int_{a=x_0}^{b=x_{2n}}f(x)dx=\frac{h}{3}\Big((y_0+4y_1+y_2)+(y_2+4y_3+y_4)+$$$$\cdots+(y_{2n-4}+4y_{2n-3}+y_{2n-2})+(y_{2n-2}+4y_{2n-1}+y_{2n})\Big)$$$$=\frac{h}{3}(y_0+4y_1+2y_2+4y_3+\cdots+2y_{2n-2}+4y_{2n-1}+y_{2n})$$
シンプソンの公式を導く
区間 $[x_1,x_3]$ を以下の2次関数で近似すると、
$$f(x)=ax^2+bx+c -②$$
この関数は3点 $(x_1,y_1)$ 、$(x_2,y_2)$ 、$(x_3,y_3)$ を通るので、
$$y_1=ax_1^2+bx_1+c -③$$$$y_2=ax_2^2+bx_2+c -④$$$$y_3=ax_3^2+bx_3+c -⑤$$
これらより係数 $a,b,c$ を求めると、(⑥~⑧の導出)
$$a=\frac{y_1-2y_2+y_3}{2h^2} -⑥$$$$b=\frac{-(x_2+x_3)y_1+2(x_1+x_3)y_2-(x_1+x_2)y_3}{2h^2} -⑦$$$$c=\frac{x_2x_3y_1-2x_1x_3y_2+x_1x_2y_3}{2h^2} -⑧$$
②を区間 $[x_1,x_3]$ で積分し、⑥~⑧を代入すると、シンプソンの公式①が得られます。(⑨の導出)
$$S_1=\int_{x_1}^{x_3}(ax^2+bx+c)dx=\frac{a}{3}(x_3^3-x_1^3)+\frac{b}{2}(x_3^2-x_1^2)+c(x_3-x_1)$$$$=\frac{h}{3}(y_1+4y_2+y_3) -⑨$$
⑥~⑧を導く
③と④および④と⑤から $c$ を消去すると、
$$(x_2-x_1)b=y_2-y_1-a(x_2^2-x_1^2) -(1)$$$$(x_3-x_2)b=y_3-y_2-a(x_3^2-x_2^2) -(2)$$
これらより $b$ を消去し、$h$ を使うと⑥が得られます。
$$a(x_3^2-x_2^2)-a(x_2^2-x_1^2)=y_3-y_2-(y_2-y_1)$$$$a=\frac{y_1-2y_2+y_3}{2h^2}$$
この $a$ を(1)に代入すると⑦が得られます。
$$hb=y_2-y_1-\frac{y_1-2y_2+y_3}{2h}(x_2+x_1)$$$$b=\frac{-(x_2+x_3)y_1+2(x_1+x_3)y_2-(x_1+x_2)y_3}{2h^2}$$
⑥と⑦を③に代入すると⑧が得られます。
$$c=y_1-\frac{y_1-2y_2+y_3}{2h^2}x_1^2$$$$-\frac{-(x_2+x_3)y_1+2(x_1+x_3)y_2-(x_1+x_2)y_3}{2h^2}x_1$$$$=\frac{x_2x_3y_1-2x_1x_3y_2+x_1x_2y_3}{2h^2}$$
⑨を導く
⑨の左辺を書き換えると、
$$S_1=2h\Big(\frac{a}{3}(x_3^2+x_1x_3+x_1^2)+\frac{b}{2}(x_3+x_1)+c\Big)$$
これに⑥~⑧を代入すると⑨が得られます。
$$hS_1=\frac{1}{3}(y_1-2y_2+y_3)(x_3^2+x_1x_3+x_1^2)$$$$+\frac{1}{2}\Big(-(x_2+x_3)y_1+2(x_1+x_3)y_2-(x_1+x_2)y_3\Big)(x_3+x_1)$$$$+x_2x_3y_1-2x_1x_3y_2+x_1x_2y_3$$$$=\frac{y_1}{6}(-x_3^2-x_1x_3+3x_2x_3+2x_1^2-3x_1x_2)+\frac{y_2}{3}(x_3^2-2x_1x_3+x_1^2)$$$$+\frac{y_3}{6}(2x_3^2-x_1x_3-x_1^2+3x_1x_2-3x_2x_3)$$$$=\frac{h^2}{3}y_1+\frac{4h^2}{3}y_2+\frac{h^2}{3}y_3$$




