カルマンフィルタ
カルマンフィルタとは、 離散的な誤差のある観測から、時間変化する量(例えばある物体の位置と速度)を推定するために用いられるフィルタです。例えば、自動運転では、加速度計やGPS情報を利用して、自動車の位置の推定に利用されています。
カルマンフィルターは、目標物の時間変化を支配する法則を活用して、目標物の位置を現在(フィルター)、未来(予測)、過去(内挿あるいは平滑化)に推定することができる。
推定対象である物理量を $x$(確率変数)、観測雑音(観測誤差)を $w$ とすると、観測値 $y$ は以下の観測方程式で定義されます。カルマンフィルタの目的は、観測値 $y$ が得られたとき、その背後にある物理量(以下、状態)$x$ を推定することです。
$$y=ax+w$$
状態モデル
観測値 $y$ が得られる状態モデルとして以下で仮定します。${\bf x}$ は $n$ 次元状態ベクトルで、$T$ は転置行列を表します。
$$y(t)={\bf a}^T{\bf x}(t)+w(t) -①$$$${\bf x}(t+1)=A{\bf x}(t)+{\bf b}v(t) -②$$
$A$ は $n\times n$ 行列、${\bf a},{\bf b}$ は $n$ 次元列ベクトルです。これらは既知の定数(時間によらず一定)とします。
また、$w$ は観測雑音(観測誤差)、$v$ はシステム雑音を表し、平均 $\bar{w},\bar{v}$ と分散 $\sigma_w^2,\sigma_v^2$ は以下のように仮定します。
$$\bar{w}\equiv E[w(t)]=0$$$$\bar{v}\equiv E[v(t)]=0$$$$\sigma_w^2\equiv E\Big[\big(w(t)-\bar{w}\big)^2\Big]$$$$\sigma_v^2\equiv E\Big[\big(v(t)-\bar{v}\big)^2\Big]$$
状態推定値
時刻 $t$ における状態 ${\bf x}$ の推定値 $\hat{\bf x}$ として、以下の2つの量を定義します。
- 事前推定値:$\hat{\bf x}(t|t-1)$
時刻 $t-1$ までの観測値 $y(i)$ に基づき、時刻 $t$ における ${\bf x}$ を推定する。$$\hat{\bf x}(t|t-1)\equiv A\hat{\bf x}(t-1)$$ - 事後推定値:$\hat{\bf x}(t)$
時刻 $t$ までの観測値 $y(i)$ に基づき、時刻 $t$ における ${\bf x}$ を推定する。$$\hat{\bf x}(t)\equiv E[x(t)]$$
また、観測値 $y$ の事前推定値は以下で与えられます。
$$\hat{y}(t|t-1)={\bf a}^T\hat{\bf x}(t|t-1) -③$$
推定誤差
状態推定誤差 ${\bf e}_x$ とは、推定値 $\hat{\bf x}$ と真の状態値 ${\bf x}$ との差として定義されます。
$${\bf e}_x(t|t-1)\equiv{\bf x}(t)-\hat{\bf x}(t|t-1) -④$$$${\bf e}_x(t)\equiv{\bf x}(t)-\hat{\bf x}(t) -⑤$$
観測値 $y$ について出力予測誤差を以下で定義します。⑦は、⑥に①と③を代入し、④を使うと得られます。
$${\bf e}_y(t)\equiv{\bf y}(t)-\hat {\bf y}(t|t-1) -⑥$$$$={\bf a}^T{\bf e}_x(t|t-1)+w(t) -⑦$$
状態推定誤差の共分散行列 $C$ は以下で定義されます。
$$C(t|t-1)\equiv E[{\bf e}_x(t|t-1){\bf e}_x^T(t|t-1)] -⑧$$$$C(t)\equiv E[{\bf e}_x(t){\bf e}_x^T(t)] -⑨$$
無相関の条件
状態推定誤差 ${\bf e}_x$ と観測値 $y$ は無相関で、$E[{\bf e}_x]=0$ であるため、以下の無相関の条件が成り立ちます。
$$E[{\bf e}_x(t)y(i)]=E[{\bf e}_x(t)]E[y(i)]=0 -⑩$$$$i=1,2,\cdots,t$$
同様の考え方で以下の無相関の条件が成り立ちます。
$$E[{\bf e}_x(t|t-1)y(i)]=0 -⑪$$$$E[{\bf e}_x(t)\hat{y}(t|t-1)]=0 -⑫$$
時系列アルゴリズム
線形予測器
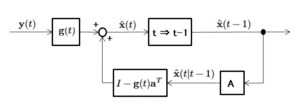
事前推定値と事後推定値について、以下のような線形予測器を仮定します。${\bf g}(t)$ はカルマンゲインといいます。
$$\hat{\bf x}(t)=G(t)\hat{\bf x}(t|t-1)+{\bf g}(t)y(t) -⑬$$
$G$ は $n\times n$ 行列、$g$ は $n$ 次元ベクトルで、以下の関係があります。
$$G(t)=I-{\bf g}(t){\bf a}^T -⑭$$
⑭の導出
直交条件⑩に⑤、⑬、①を代入すると、
$$E[{\bf e}_x(t)y(i)]=E\Big[\Big({\bf x}(x)-G(t)\hat{x}(t|t-1)-{\bf g}(t)\big({\bf a}^Tx(t)+w(t)\big)\Big)y(i)\Big]$$
$w(t)$ と $y(i)$ は独立であるから $E[w(t)y(i)]=E[w(t)]E[y(i)]=0$ と、⑩を使うと、
$$E[{\bf e}_x(t)y(i)]=E\Big[\Big({\bf x}(x)-G(t)\hat{x}(t|t-1)-{\bf g}(t){\bf a}^Tx(t)\Big)y(i)\Big]$$$$=E\Big[\Big(I-{\bf g}(t){\bf a}^T-G(t)\Big){\bf x}(t)y(i)+G(t){\bf e}_x(t|t-1)y(i)\Big]$$$$=E\Big[\Big(I-{\bf g}(t){\bf a}^T-G(t)\Big){\bf x}(t)y(i)\Big]$$$$=\Big(I-{\bf g}(t){\bf a}^T-G(t)\Big)E[{\bf x}(t)y(i)]=0$$
$E[{\bf x}(t)y(i)]\ne0$ であるため⑭が得られます。
$$G(t)=I-{\bf g}(t){\bf a}^T \to⑭$$
状態推定手順
カルマンフィルタは以下のステップによって計算します。
- 初期値 $\hat{\bf x}(0)$ の設定
$$\hat{\bf x}(0)=E[{\bf x}(0)]\equiv{\bf x}_0$$$$C(0)=E\Big[\Big({\bf x}(0)-E[{\bf x}(0)]\Big)^2\Big]\equiv{\bf \sigma}_0^2$$ - 事前推定値 $\hat{x}(t|t-1)$ の計算
$$\hat{\bf x}(t|t-1)=A\hat{\bf x}(t-1) -⑮$$$$C(t|t-1)=AC(t-1)A^T+\sigma_v^2{\bf b}{\bf b}^T -⑯$$ - 事後推定値 $\hat{x}(t)$ の計算
$$\hat{\bf x}(t)=\hat{\bf x}(t|t-1)+g(t)\Big(y(t)-{\bf a}^T\hat{\bf x}(t|t-1)\Big) -⑰$$$$C(t)=\Big({\bf 1}-g(t){\bf a}^T\Big)C(t|t-1) -⑱$$$$g(t)=\frac{C(t|t-1){\bf a}}{{\bf c}^TC(t|t-1){\bf a}+\sigma_w^2} -⑲$$
尚、⑮は事前推定値の定義です。また、⑰は⑭を⑬に代入することにより得られます。
⑯の導出
④に②と⑮を代入すると、
$${\bf e}_x(t|t-1)={\bf x}(t)-\hat{\bf x}(t|t-1)=A{\bf x}(t-1)+{\bf b}v(t-1)-A\hat{\bf x}(t-1)$$$$=A{\bf e}_x(t-1)+{\bf b}v(t-1)$$
これを⑧に代入すると、
$$C(t|t-1)=E\Big[\Big(A{\bf e}_x(t-1)+{\bf b}v(t-1)\Big)\Big(A{\bf e}_x(t-1)+{\bf b}v(t-1)\Big)^T\Big]$$$$=AE[{\bf e}_x(t-1){\bf e}_x^T(t-1)]A^T+AE[{\bf e}_x(t-1)v(t-1)]{\bf b}^T$$$$+{\bf b}E[v(t-1){\bf e}_x^T(t-1)]A^T+{\bf b}E[v^2(t-1)]{\bf b}^T$$
第2項と第3項は $v$ と ${\bf e}_x$ が無相関であるため0となり、⑨を使うと⑯が得られます。
$$C(t|t-1)=AC(t-1)A^T+\sigma_v^2{\bf b}{\bf b}^T \to⑯$$
⑱の導出
⑨に⑳を代入すると、
$$C(t)=E\Big[\Big(\big(I-{\bf g}(t){\bf a}^T\big){\bf e}_x(t|t-1)-{\bf g}(t)w(t)\Big)$$$$\times\Big(\big(I-{\bf g}(t){\bf a}^T\big){\bf e}_x(t|t-1)-{\bf g}(t)w(t)\Big)^T\Big]$$$$=\big(I-{\bf g}(t){\bf a}^T\big)E\Big[{\bf e}_x(t|t-1){\bf e}_x^T(t|t-1)\Big]\big(I-{\bf g}(t){\bf a}^T\big)^T$$$$-\big(I-{\bf g}(t){\bf a}^T\big)E\Big[{\bf e}_x(t|t-1)w(t)\Big]{\bf g}^T(t)$$$$-{\bf g}(t)E\Big[w(t){\bf e}_x^T(t|t-1)\Big]\big(I-{\bf g}(t){\bf a}^T\big)^T+{\bf g}(t)E\Big[w^2(t)\Big]{\bf g}(t)^T$$
第2項と第3項は $w$ と ${\bf e}_x$ が無相関であるため0となり、⑧と㉑を使うと⑱が得られます。
$$C(t)=\big(I-{\bf g}(t){\bf a}^T\big)C(t|t-1)\big(I-{\bf g}(t){\bf a}^T\big)^T+\sigma_w^2{\bf g}(t){\bf g}(t)^T$$$$=\big(I-{\bf g}(t){\bf a}^T\big)C(t|t-1)-\big(I-{\bf g}(t){\bf a}^T\big)C(t|t-1){\bf a}{\bf g}^T(t)+\sigma_w^2{\bf g}(t){\bf g}(t)^T$$$$=\big(I-{\bf g}(t){\bf a}^T\big)C(t|t-1) \to⑱$$
⑲の導出
⑤に⑰と①を代入し、④を使うと、
$${\bf e}_x(t)={\bf x}(t)-\hat{\bf x}(t|t-1)-{\bf g}(t)\Big({\bf a}^T{\bf x}(t)+w(t)-{\bf a}^T\hat{\bf x}(t|t-1)\Big)$$$$={\bf e}_x(t|t-1)-{\bf g}(t)\Big({\bf a}^T{\bf e}_x(t|t-1)+w(t)\Big)$$$$=\Big(I-{\bf g}(t){\bf a}^T\Big){\bf e}_x(t|t-1)-{\bf g}(t)w(t) -⑳$$
⑫に⑩を使うと、
$$E[{\bf e}_x(t)\hat{y}(t|t-1)]=E[{\bf e}_x(t){\bf e}_y(t)]=0$$
これに⑦と⑳を代入すると、
$$E\Big[\Big(\big(I-{\bf g}(t){\bf a}^T\big){\bf e}_x(t|t-1)-{\bf g}(t)w(t)\Big)\Big({\bf a}^T{\bf e}_x(t|t-1)+w(t)\Big)\Big]$$$$=\Big(I-{\bf g}(t){\bf a}^T\big)E\Big[{\bf e}_x(t|t-1)\Big({\bf a}^T{\bf e}_x(t|t-1)\Big)\Big]-{\bf g}(t){\bf a}^TE\Big[w(t){\bf e}_x(t|t-1)\Big]$$$$+\Big(I-{\bf g}(t){\bf a}^T\Big)E\Big[{\bf e}_x(t|t-1)w(t)\Big]-{\bf g}(t)E\Big[w^2(t)\Big]=0$$
この第2項と第3項は0になり、第1項と第4項を書き換えると、
$$\Big(I-{\bf g}(t){\bf a}^T\big)E\Big[{\bf e}_x(t|t-1){\bf e}_x^T(t|t-1)\Big]{\bf a}-{\bf g}(t)\sigma_w^2=0$$
これに⑧を代入すると⑲が得られます。
$$\Big(I-{\bf g}(t){\bf a}^T\big)C(t|t-1){\bf a}-{\bf g}(t)\sigma_w^2=0 -㉑$$$${\bf g}(t)=\frac{C(t|t-1){\bf a}}{{\bf a}^tC(t|t-1){\bf a}+\sigma_w^2} \to⑲$$