ブール代数
ブール代数とは、真(truth)と 偽(false)または「1」(信号あり)と「0」(信号なし)の2つの値のみを用いて論理演算を行う数学体系で、AND(論理積)、OR(論理和)、NOT(論理否定)などの基本演算により、コンピュータの論理回路設計の基礎となります。
ブール代数の主な公理と定理は以下になります。ここで、$A\sim C$ は2値をとる変数、「 $\cdot$ 」は論理積、「 $+$ 」は論理和、$\overline{A}$ は $A$ の論理否定を表します。
| 公理 | $\overline{1}=0$ 、$\overline{0}=1$ $A\cdot 0=0$ 、$A+1=A$ |
| 単位元則 | $A\cdot 1=A$ 、$A+0=A$ |
| 補元則 | $A\cdot\overline{A}=0$ 、$A+\overline{A}=1$ |
| 対合則 | $\overline{\overline{A}}=A$ |
| べき等則 | $A\cdot A\cdot\,\cdots\,\cdot A=A$ $A+A+\,\cdots\,+A=A$ |
| 交換則 | $A\cdot B=B\cdot A$ $A+B=B+A$ |
| 結合則 | $(A\cdot B)\cdot C=A\cdot(B\cdot C)$ $(A+B)+C=A+(B+C)$ |
| 分配則 | $A\cdot (B+C)=A\cdot B+A\cdot C$ $(A+B)\cdot(A+C)=A+B\cdot C$ |
| 吸収則 | $A\cdot(A+B)=A+A\cdot B=A$ $A+\overline{A}\cdot B=A+B$ $\overline{A}+A\cdot B=\overline{A}+B$ |
| ド・モルガンの法則 | $\overline{A\cdot B}=\overline{A}+\overline{B}$ $\overline{A+B}=\overline{A}\cdot\overline{B}$ |
分配則と吸収則については直感的に分かりにくいので、以下に真理値表を載せます。
- 分配則
$A$ $B$ $C$ $(A+B)\cdot(A+C)$ $A+B\cdot C$ 0 0 0 (0+0)・(0+0)=0 0+0・0=0 0 0 1 (0+0)・(0+1)=0 0+0・1=0 0 1 0 (0+1)・(0+0)=0 0+1・0=0 0 1 1 (0+1)・(0+1)=1 0+1・1=1 1 0 0 (1+0)・(1+0)=1 1+0・0=1 1 0 1 (1+0)・(1+1)=1 1+0・1=1 1 1 0 (1+1)・(1+0)=1 1+1・0=1 1 1 1 (1+1)・(1+1)=1 1+1・1=1 - 吸収則
$A$ $B$ $A+\overline{A}\cdot B$ $A+B$ 0 0 0+1・0=0 0+0=0 0 1 0+1・1=1 0+1=1 1 0 1+0・0=1 1+0=1 1 1 1+0・1=1 1+1=1 $A$ $B$ $\overline{A}+A\cdot B$ $\overline{A}+B$ 0 0 1+0・0=1 1+0=1 0 1 1+0・1=1 1+1=1 1 0 0+1・0=0 0+0=0 1 1 0+1・1=1 0+1=1
論理回路
デジタル回路では、電気信号は High レベル(高電圧)と Low レベル(低電圧)の2つの値しか許されません。ブール代数の「1」と「0」を電気信号の High レベルと Low レベルで置き替えることにより、デジタル回路でブール代数に従った論理演算を行うことができます。
回路記号
1端子入力
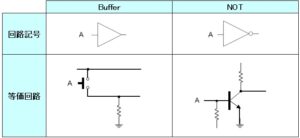
1端子入力で、入力値 A をそのまま出力する回路を Buffer 、論理否定を出力する回路を NOT と呼びます。以下はその真理値表です。
| 入力 | 出力 | |
| $A$ | Buffer | NOT |
| $A$ | $\overline{A}$ | |
| 0 | 0 | 1 |
| 1 | 1 | 0 |
回路記号と等価回路は以下になります。
2端子入力
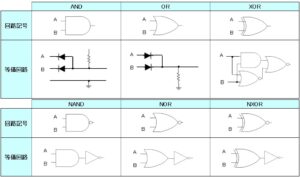
2端子入力で、入力値 A 、B の論理積を出力する回路を AND 、論理和を出力する回路を OR 、排他論理和を出力する回路を XOR 、そして、それぞれの論理否定を出力する回路を NAND 、NOR 、XNOR と呼びます。以下はその真理値表です。
| 入力 | 出力 | ||||||
| $A$ | $B$ | AND | XOR | OR | NOR | XNOR | NAND |
| $A\cdot B$ | $A\oplus B$ | $A+B$ | $\overline{ A+B}$ | $\overline{ A\oplus B}$ | $\overline{ A\cdot B}$ | ||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | ||||||
| 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 |
回路記号と等価回路は以下になります。
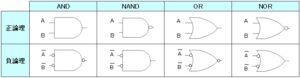
正論理と負論理
正論理(アクティブハイ)は、「1」(信号あり)を電気信号の High レベル(高電圧)とする論理系で、負論理(アクティブロー)は、Low レベル(低電圧)とする論理系です。回路設計において、ノイズ対策や消費電力の観点から負論理が使われる場合があります。
| 論理系 | 正論理 | 負論理 |
| 真「1」 | High レベル | Low レベル |
| 偽「0」 | Low レベル | High レベル |
デジタル回路の表記では、負論理の信号を $\overline{A}$ のようにバーを付けて表し、負論理の信号を接続する論理記号の端子に “〇” を付けて表します。基本的には、正論理の信号は正論理の端子に接続し、負論理の信号は負論理の端子に接続させることが推奨されます。