光子の伝播関数とは
伝播関数とは、ある時刻での場の演算子の期待値が、別の時刻での場の演算子の期待値にどのように影響(伝搬)するかを示す量です。伝播関数は、電磁場のベクトルポテンシャル $A_\mu$ とボソンの時間順序積( $T$ 積)により以下で表されます。
$$D_F^{\mu\nu}(k)=\braket{0|T\big(A_\mu(x)A_\nu(x’)\big)|0}$$
尚、時間順序積は以下で定義されます。
$$T\big(A_\mu(x)A_\nu(x’)\big)\equiv\left\{\begin{array}{ll}
A_\mu(x)A_\nu(x’) & (t\gt t’) -①\\
A_\nu(x’)A_\mu(x) & (t’\gt t) -②\end{array} \right.$$
電磁場のベクトルポテンシャル ${\bf A}$ をフーリエ展開すると、
$${\bf A}({\bf x},t)=\frac{1}{\sqrt{V}}\sum_k\sum_{\alpha=1,2}\Big(c_{k,\alpha}u_{k,\alpha}({\bf x})+c_{k,\alpha}^*u_{k,\alpha}^*({\bf x})\Big)$$$$u_{k,\alpha}({\bf x})=\epsilon^\alpha e^{ik\cdot x}$$
これを量子化すると以下で表されます。尚、$\epsilon^\alpha$ は偏極を表す実数の単位ベクトルです。
$$A_\mu=\frac{1}{\sqrt{V}}\sum_k\sum_\alpha c\sqrt{\frac{\hbar}{2\omega}}\Big(\epsilon_\mu^\alpha a_{k\alpha}e^{ik\cdot x}+\epsilon_\mu^\alpha a_{k\alpha}^\dagger e^{-ik\cdot x}\Big) -③$$
以降は $c=\hbar=1$ と置きます。このとき、光子の伝播関数は以下で表されます。
$$\braket{0|T\big(A_\mu(x)A_\nu(x’)\big)|0}=\frac{-i}{(2\pi)^4}\delta_{\mu\nu}\int d^4k\frac{e^{ik\cdot(x-x’)}}{k^2-i\epsilon} -④$$
光子の伝播関数を導く
まず、$t\gt t’$ の場合は③を①に代入すると、
$$\braket{0|T\big(A_\mu(x)A_\nu(x’)\big)|0}=\frac{1}{V}\sum_{kk’}\sum_{\alpha\alpha’}\frac{1}{2\sqrt{\omega\omega’}}\epsilon_\mu^\alpha\epsilon_\nu^{\alpha’}e^{i(k\cdot x-k’\cdot x’)}\braket{0|a_{k\alpha}a_{k’\alpha’}^\dagger|0}$$$$=\frac{1}{V}\sum_k\sum_\alpha\frac{1}{2\omega}\epsilon_\mu^\alpha\epsilon_\nu^\alpha e^{ik\cdot(x-x’)}$$$$=\int\frac{d^3k}{(2\pi)^3}\frac{\delta_{\mu\nu}}{2\omega}e^{ik\cdot(x-x’)-i\omega(t-t’)} -⑤$$
最後は、電磁場において $\epsilon^1$ 、$\epsilon^2$ 、$\epsilon^3$($={\bf k}/k$)は互いに直交するため、
$$\sum_{\alpha=1}^3\epsilon_\mu^\alpha\epsilon_\nu^\alpha=\delta_{\mu\nu}$$
また、$V\to\infty$ で以下のように置き換えています。尚、$k^2=|{\bf k}|^2-k_0^2$ 、$k_0\simeq\omega$ です。
$$\lim_{V\to\infty}\frac{1}{V}\sum_k=\int\frac{d^3k}{(2\pi)^3}$$
一方、$t’\gt t$ の場合は③を②に代入すると、同様に、
$$\braket{0|T\big(A_\nu(x’)A_\mu(x)\big)|0}=\int\frac{d^3k}{(2\pi)^3}\frac{\delta_{\mu\nu}}{2\omega}e^{ik\cdot(x’-x)-i\omega(t’-t)} -⑥$$
また、④の $k$ を書き直し、$k_0$ の虚数部を $\delta$ と置くと、
$$④=\frac{-i}{(2\pi)^4}\delta_{\mu\nu}\int d^3k\int dk_0\frac{e^{ik\cdot(x-x’)-ik_0(t-t’)}}{-(k_0-\omega+i\delta)(k_0+\omega-i\delta)} -⑦$$
この被積分関数は、第2象限($k_0=-\omega+i\delta$)と第4象限($k_0=\omega-i\delta$)に極を持つことが分かります。この積分は、以下のコーシーの積分表示を使います。右辺の符号は、周回積分が左回りの場合に正符号、右回りの場合に負符号になります。
$$\oint\frac{f(z)}{(z-z_0)}dz=\pm2\pi if(z_0) -⑧$$
⑦から⑤の導出
$t\gt t’$ の場合、⑦の $k_0$ による積分は、$\mathrm{Im}(k_0)\gt0$ で $e^{-ik_0(t-t’)}$ は寄与を持って(無限大に発散して)しまうため、複素平面上の積分路を実軸と下半円(負側)で構成します。
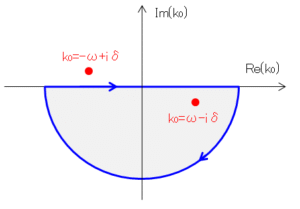
この場合は、第4象限($k_0=\omega-i\delta$)の極から寄与のみとなります。
$$f(k_0)=\frac{e^{ik\cdot(x-x’)-ik_0(t-t’)}}{k_0+\omega-i\delta}$$
と置いて、⑦を書き換え、コーシーの積分表示(右回りのため負符号)を利用すると、
$$⑦=\frac{-i}{(2\pi)^4}\delta_{\mu\nu}\int d^3k\int dk_0\frac{f(k_0)}{-(k_0-\omega+i\delta)}$$$$=\frac{1}{(2\pi)^3}\delta_{\mu\nu}\int d^3k\frac{e^{ik\cdot(x-x’)-i(\omega-i\delta)(t-t’)}}{2\omega-2i\delta}$$
ここで $\delta\to0$ とすると⑤が得られます。
$$⑦\simeq\frac{1}{(2\pi)^3}\delta_{\mu\nu}\int d^3k\frac{e^{ik\cdot(x-x’)-i\omega(t-t’)}}{2\omega} \to⑤$$
⑦から⑥の導出
$t’\gt t$ の場合、⑦の $k_0$ による積分は、$\mathrm{Im}(k_0)\lt0$ で $e^{-ik_0(t-t’)}$ は寄与を持って(無限大に発散して)しまうため、複素平面上の積分路を実軸と上半円(正側)で構成します。
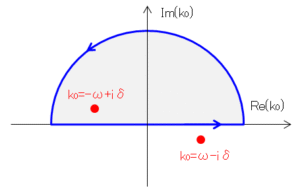
この場合は、第2象限($k_0=-\omega+i\delta$)の極から寄与のみとなります。
$$f(k_0)=\frac{e^{ik\cdot(x-x’)-ik_0(t-t’)}}{-(k_0-\omega+i\delta)}$$
と置いて、⑦を書き換え、コーシーの積分表示(左回りのため正符号)を利用すると、
$$⑦=\frac{-i}{(2\pi)^4}\delta_{\mu\nu}\int d^3k\int dk_0\frac{f(k_0)}{k_0+\omega-i\delta}$$$$=\frac{1}{(2\pi)^3}\delta_{\mu\nu}\int d^3k\frac{e^{ik\cdot(x-x’)-i(-\omega+i\delta)(t-t’)}}{-(-2\omega+2i\delta)}$$
ここで $\delta\to0$ とし、${\bf k}\to-{\bf k}$ と置き換えると⑥が得られます。
$$⑦\simeq\frac{1}{(2\pi)^3}\delta_{\mu\nu}\int d^3k\frac{e^{ik\cdot(x’-x)-i\omega(t’-t)}}{2\omega} \to⑥$$




