ベイズの定理
ベイズの定理とは、ある事象の確率 $P$ を、その事象に関連する条件の知識に基づいて求める手法です。ベイズの定理は、パターン認識や機械学習において、中心的な役割を果たします。
事象 $X$ が起きる確率 $P(X)$ とすると、ベイズの定理は以下のように表されます。
| $$P(Y|X)=\frac{P(X|Y)P(Y)}{P(X)}$$ |
ここで、$P(Y|X)$ と $P(X|Y)$ は条件付き確率で、次の意味を持ちます。
- $P(Y|X)$:事象 $X$ の条件下で事象 $Y$ が起きる確率。
- $P(X|Y)$:事象 $Y$ の条件下で事象 $X$ が起きる確率。
ベイズの定理を導く前提となる、確率の基本定理について述べます。
加法定理と乗法定理
加法定理は、個別の事象が起きる確率と同時確率との関係を表します。同時確率とは、事象 $X$ と事象 $Y$ が同時に起きる確率 $P(X,Y)$ です。
$$P(X)=\sum_YP(X,Y)$$
乗法定理は、同時確率と条件付き確率との関係を表します。
$$P(X,Y)=P(X|Y)P(Y)$$
3つの定理を導く
3つの定理を導きます。下図では確率を”面積”でイメージ化しています。
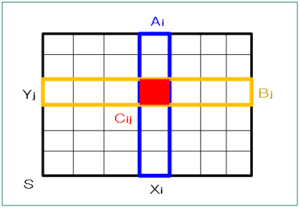
事象 $X_i$ の起きる確率は青枠の面積 $A_i$、事象 $Y_j$ の起きる確率は黄枠の面積 $B_j$、同時確率は赤部の面積 $C_{ij}$ にそれぞれ比例するとします。全体の面積を $S$ として、各確率を以下で定義します。
$$P(X_i)=\frac{A_i}{S} , P(Y_j)=\frac{B_j}{S}$$$$P(X_i,Y_j)=\frac{C_{ij}}{S}$$$$P(Y_j|X_i)=\frac{C_{ij}}{A_i} , P(X_i|Y_j)=\frac{C_{ij}}{B_j}$$
$A_i$ は $C_{ij}$ の全て $j$ のについて足し合わせたものなので、これから加法定理が導かれます。
$$A_i=\sum_jC_{ij}$$$$P(X_i)=\sum_jP(X_i,Y_j)$$
また、乗法定理は以下のように導くことができます。
$$P(X_i,Y_j)=\frac{C_{ij}}{S}=\frac{C_{ij}}{B_i}\frac{B_i}{S}=P(X_i|Y_j)P(Y_j)$$
乗法定理は $X$ と $Y$ を入れ替えても成り立ちますので、
$$P(Y,X)=P(X,Y)$$$$P(Y|X)P(X)=P(X|Y)P(Y)$$
両辺を $P(X)$ で割るとベイズの定理を導くことができます。
ベイズ推定
ベイズ推定とは、ベイズの定理を基に、観測された事象の確率(事前確率)から、知りたい事象の確率(事後確率)を推定することです。
$$P(Y|X)=\frac{P(X|Y)P(Y)}{P(X)}$$
ここで、$P(Y)$ が事前確率、$P(Y|X)$ が事後確率です。$P(X|Y)$ は尤度(ゆうど)関数と呼ばれています。尚、$P(X)$ は規格化定数として取り扱われ、加法定理と乗法定理から求められます。
$$P(X)=\sum_YP(X|Y)P(Y)$$
従って、ベイズ推定は以下のように書き換えることができます。
$$P(Y|X)=\frac{P(X|Y)P(Y)}{\sum_YP(X|Y)P(Y)}$$
迷惑メールの判定の例
ある会社に届いた電子メールが、迷惑メールかどうかの判定を、メールに含まれる特定文字列を基に判定するとします。この特定文字列は「大売出し」のような怪しい文言であるとします。
迷惑メールである事象を $Y_1$、そうでない事象を $Y_0$、また特定文字列が含まれる事象を $X_1$、含まれない事象を $X_0$ をとします。
今受け取った電子メールに特定文字列が含まれた場合、それが迷惑メールである確率 $P(Y_1|X_1)$ は、過去の迷惑メールと特定文字列のデータより求めることができます。
$$P(Y_1|X_1)=\frac{P(X_1|Y_1)P(Y_1)}{P(X_1|Y_0)P(Y_0)+P(X_1|Y_1)P(Y_1)}$$




